Non-diffusive atmospheric flow #3: reanalysis data and Z500
In this article, we’re going to look at some of the details of the data that we’re going to be using in our study of non-diffusive flow in the atmosphere. This is still all background material, so there’s no Haskell code here!
Reanalysis data
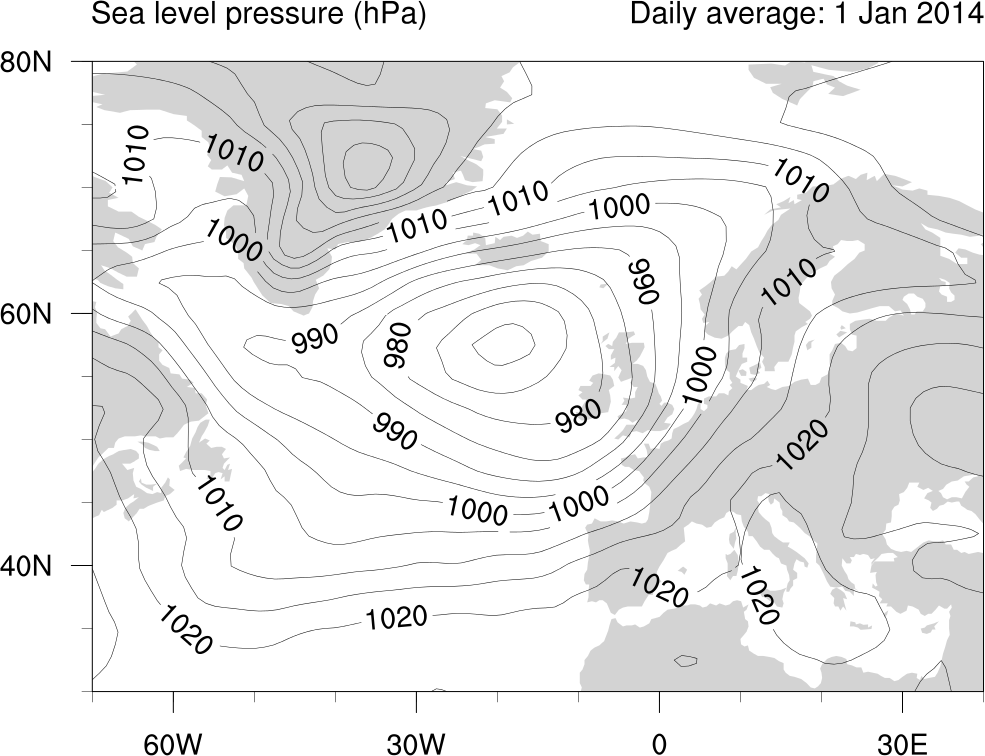
In the last article, we talked blithely about looking at “patterns” in the atmosphere. By “patterns”, we mean patterns of atmospheric flow–for example, we might be interested in looking at differences between times when the normal conditions of westerly winds over the North Atlantic prevail and times when those conditions are interrupted and the winds are doing something else (those two states are associated with different kinds of weather over Northern Europe). The easiest way to think about these spatial patterns is by thinking of the isobars (lines of constant pressure) on a conventional weather map, the kind of thing you might see on the news. This plot shows daily mean sea level pressure over the North Atlantic for 1 January 2014, showing a low pressure system just south of Iceland. The contours are labelled in hPa (i.e. 100 Pascals), which correspond pretty closely to the more “traditional” units of millibars (1000 hPa ≈ 1000 mb):
Because of the rotation of the Earth, in the Northern Hemisphere the winds flow anticlockwise around regions of low pressure, clockwise around regions of high pressure, and are stronger in areas where the pressure gradient is greater (i.e. where the isobars are closer together).
But how do you even measure enough spatial points in the atmosphere to make a smooth-looking map like this? We can measure temperature, rainfall and wind speed and direction at surface weather stations, but they give just a few point measurements (and they’re very unevenly distributed around the globe). We can use instruments on satellites to measure some quantities, although getting from what the instruments measure (basically visible or infra-red radiation in different frequency bands) to the quantities of interest is very difficult and is a whole data analysis problem of its own. Even then, you only get direct measurements below the satellite’s orbital track. For a satellite in a polar orbit, that means (more or less) two measurements per day at each point on the globe.
To produce a global picture requires something more. The “something more” is usually a model of what’s going on. If you have a good computational model of a system, it’s possible to use a technique called data assimilation to combine measurements and modelling to get a “best guess” view of the state of the system. In the case of the atmosphere, numerical weather prediction models have reached a pretty high state of sophistication and most of the large national weather centres use one of these models combined with as much satellite, ground and other observational data they can get their hands on, in order to produce an “analysis” state of the atmosphere. Here, “analysis” basically means best guess of the current state given what we know from the past, what our model tells us and what observational data we have up to this point in time.
And this is where we get the data we’re going to use. There are a couple of atmospheric reanalysis projects, which try to take the best models we currently have and all the historical observational data of various kinds that are available and of high enough quality, in order to produce a historical “reanalysis” of the state of the atmosphere at any given time. This historical reanalysis is not an exact picture of the state of the atmosphere over time for a host of reasons. Some variables are intrinsically hard to predict, like rainfall. Some other variables are influenced by strong nonlinearities, both in the atmosphere itself (tropical convection is a good example) and in the interaction between the surface and the lower regions of the atmosphere (the difference between the reflectivity of sea ice and open ocean is a big one here). And other problems are caused by the finite spatial and temporal resolution of the model used. In any case, the reanalysis gives a fairly accurate representation of the state of the atmosphere, better than could be achieved by modelling or isolated observations alone.
The reanalysis data we’re going to use is generated by the National Centers for Environmental Prediction and the National Center for Atmospheric Research (NCEP/NCAR). It covers the period from 1948 to the present day and contains dozens of atmospheric and surface variables.
The geopotential height and $Z_{500}$
The plot above shows the sea level pressure, but we’re going to use a slightly different variable for our analysis. For a given pressure $p$, the geopotential height at pressure $p$, denoted $Z_p$, is the altitude (which we’ll measure in metres) of the surfaces of constant pressure $p$. In particular, we’ll be concentrating on $Z_{500}$, the geopotential height at 500 mb (millibars, which is about the same as 500 hPa: most people switch back and forth between the two units without even worrying about conversion factors too much).
Let’s think a little bit about why this is an interesting variable to look at. Atmospheric pressure at sea level is about 1000 millibars, the exact value depending on the state of the atmosphere. So 500 millibars is about half-way up the atmosphere, from the surface to the vacuum of space, as measured in pressure coordinates. At an altitude of $Z_{500}$ (which is usually a little above 5000 m) , where the pressure is 500 mb, half of the atmosphere by mass is below and half above. This is an interesting level for three reasons. First, it’s a level above where most of the “weather” happens. Second, although changes at this level tend to reflect weather-like phenomena, the details tend to be smoothed out spatially, allowing us to take a larger-scale view of the spatial patterns in the atmospheric flow. Finally, it’s an interesting level simply by virtue of being “half way up”.
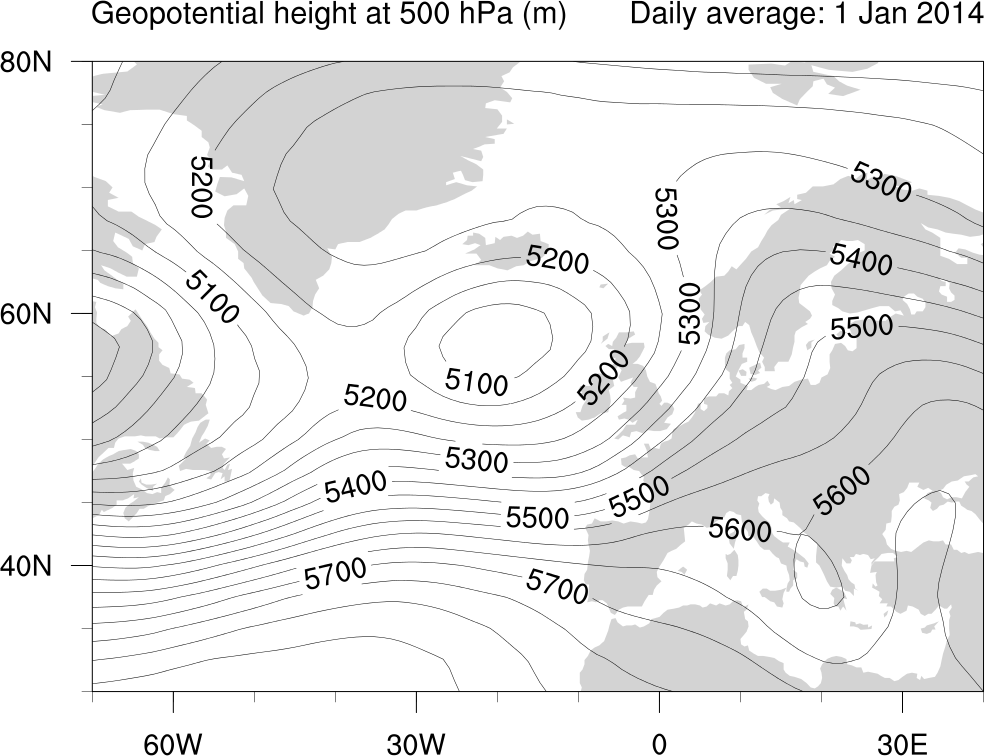
Here’s a plot of the $Z_{500}$ field for the North Atlantic from 1 Janurary 2014, the same day as that for which the top figure shows the sea level pressure (the contours are labelled in metres):
Think of a tank filled with two immiscible liquids of different densities, oil and water say. If we dye the bottom layer blue, we’ll be able to see what’s going on more clearly. If we tip the tank back and forth a little, we’ll be able to excite waves on the top surface of the top liquid layer, but we’ll also see waves on the interface between the two liquid layers. Although it’s only a weakish analogy, you can think of the disturbances we can see in the $Z_{500}$ field as being a little like those interfacial waves. (The analogy is weak because of what happens at the top surface: the atmosphere doesn’t have one!)
Comparing the SLP and $Z_{500}$ plots, you can see more or less the same features in the pattern of atmospheric flow (remember that the pressure distribution says something about the winds, so it really does make sense to speak of this as a pattern of atmospheric “flow”). In places where the sea level pressure is lower, the 500 mb geopotential height level is depressed–you can think of this as there being less “total atmosphere” over a particular sea level point, which means “half way up” isn’t as high. Some of the details in the sea level pressure plot are smoothed out in the $Z_{500}$ plot, demonstrating the larger-scale structure that the $Z_{500}$ field captures. For instance, the isolated high pressure area over eastern Greenland visible in the sea level pressure plot is smoothed out in the $Z_{500}$ plot.
So, $Z_{500}$ is the variable we’re going to look at. In the next article, I’ll show you some of the features we can see in this field in the NCEP reanalysis data set, which will help to make it a little clearer why this is going to be a useful thing to do.