Lyapunov Exponents in Haskell: Part 1
The archetypal chaotic dynamical system is the Lorentz system, defined by the differential equation system
where
Determining whether a given dynamical system will exhibit chaotic behaviour is, in general, difficultIn fact, the Lorenz system was only proven to be chaotic in 2002–see: W. Tucker (2002). A rigorous ODE solver and Smale’s 14th problem. Found. Comp. Math. 2(1), 53-117 (PDF).. The orbit structure of chaotic systems can be very complex, and it can be difficult to distinguish true chaos from a number of related phenomena.
One approach to characterising the orbit structure of dynamical systems is via Lyapunov exponents, a spectrum of values that measure the stretching and squashing of orbits–“normal” chaotic systems normally have at least one positive Lyapunov exponent and are dissipative, which means that the sum of all of their Lyapunov exponents is negative. While it is relatively straightforward to define Lyapunov exponents, in practice calculating them is tricky. We’ll see how to do this in some practical cases in this and the next couple of articles, following mostly the approach of Rangarajan et al. (1998).
The motivation for this series of articles was basically that I have recently been wondering about how practical it would be to use Haskell for more “traditional” mathematics: there is a big body of work and code relating to category theory and type theory in Haskell, but I’ve not seen so much about matrix algebra, differential equations, dynamical systems and so on. I implemented the Rangarajan method in Mathematica some years ago and thought it might be a good test case. I’m going to gloss over a lot of technical details about the computation of Lyapunov exponents since my main interest is in the Haskell implementation issues.
What are Lyapunov exponents?
Consider a continuous dynamical system
with
where
We can integrate this linearised equation along the reference trajectory to get the fundamental solution matrix
The Lyapunov exponents measure the rate of divergence (or convergence) of nearby solutions to the original system of differential equations.
In order to calculate the Lyapunov exponents for a system, the approach that we will follow is to find an explicit representation for the matrix
Decomposition of the fundamental solution matrix
The columns of the matrix
The key to the approach of Rangarajan et al. is to develop a suitable decomposition of the matrix
$$\dot{Q} R + Q \dot{R} = \nabla F \; QR.$$
Multiplying on the left by $Q^T$ and on the right by $R^{-1}$, we get
$$Q^T \dot{Q} + \dot{R} R^{-1} = Q^T \nabla F \; Q.$$
The two terms on the left hand side have a special structure that will be helpful: $Q^T \dot{Q}$ is skew symmetricAs can be seen by differentiating $Q^T Q = I$, the definition of an orthogonal matrix., while $\dot{R} R^{-1}$ is still upper triangularBoth $\dot{R}$ and $R^{-1}$ are upper triangular and thus so is their product.. We’ll call this our “basic equation”, since it’s what we’re going to use to develop a system we can solve for the Lyapunov exponents.
Representation of orthogonal matrices
We now choose an explicit representation for the orthogonal matrix $Q$. In $n$ dimensions, a rotation matrix is characterised by $n(n-1)/2$ parameters, which we can choose to be angles $\theta_{ij}$ representing simple rotations in the planes spanned by coordinates $x_i$ and $x_j$ (with $i < j$). A simple rotation in the $(i,j)$ plane is then represented by the matrix
$$O^{(ij)}_{kl} = \begin{cases} 1 & \text{if } k = l \neq i, j; \\ \cos \theta_{ij} & \text{if } k = l = i \;\text{ or } j; \\ \sin \theta_{ij} & \text{if } k = i, l = j; \\ -\sin \theta_{ij} & \text{if } k = j, l = i; \\ 0 & \text{otherwise}. \end{cases}$$
The full orthogonal matrix $Q$ is then
$$Q = O^{(12)} O^{(13)} \cdots O^{(1n)} O^{(23)} \cdots O^{(n-1,n)}.$$
Below, we will also label the $\theta_{ij}$ angles as $\theta_k$, $1 \leq k \leq n(n-1)/2$ in the order the $O^{(ij)}$ matrices are used in the definition of $Q$.
We can use this explicit representation of $Q$ in terms of the $\theta_k$ to calculate $Q^T \dot{Q}$ on the left hand side of the evolution equation for
$$Q^T \dot{Q} = \begin{pmatrix} 0 & -f_{21}(\theta, \dot{\theta}) & -f_{31}(\theta, \dot{\theta}) & \cdots & -f_{n1}(\theta, \dot{\theta}) \\ f_{21}(\theta, \dot{\theta}) & 0 & -f_{32}(\theta, \dot{\theta}) & \cdots & -f_{n2}(\theta, \dot{\theta}) \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ f_{n1}(\theta, \dot{\theta}) & f_{n2}(\theta, \dot{\theta}) & f_{n3}(\theta, \dot{\theta}) & \cdots & 0 \end{pmatrix}$$
In general, the entries in the matrix $Q^T \dot{Q}$ consist of terms involving products of sines and cosines of the $\theta_k$ plus a single $\dot{\theta}_k$ derivative factor. We can extract the lower diagonal entries of $Q^T \dot{Q}$, evaluate the sines and cosines to give linear expressions involving the $\dot{\theta}_k$, then solve for the $\dot{\theta}_k$ using the corresponding lower diagonal entries from the right hand side matrix $Q^T \nabla F \; Q$.
Putting it all together
We also need a representation for the upper triangular matrix $R$. We’re actually only interested in the on-diagonal elements of this matrix, so we write
$$R = \begin{pmatrix} e^{\lambda_1} & r_{12} & \cdots & \cdots & r_{1n} \\ 0 & e^{\lambda_2} & r_{23} & \cdots & r_{2n} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & e^{\lambda_n} \end{pmatrix}$$
The form of the diagonal entries ensures that they are positive (as required), but also handles the issue of exponential scaling arising from the stretching and squashing of phase space volumes–the quantities we’re going to be interested in are actually the $\lambda_i$, which turn out to be closely related to the Lyapunov exponents–in fact, the $i$th Lyapunov exponent is $\lim_{t\to\infty} \lambda_i(t)/t$. The matrix $R$ appears in the evolution equation for the fundamental solution matrix in the form
$$\dot{R} R^{-1} = \begin{pmatrix} \dot{\lambda_1} & r’_{12} & \cdots & \cdots & r’_{1n} \\ 0 & \dot{\lambda_2} & r’_{23} & \cdots & r’_{2n} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \dot{\lambda_n} \end{pmatrix}$$
where the $r’_{ij}$ are values that we’re not particularly interested in here. We then have what we need for the left hand side of our “basic equation”:
where, again, the
To integrate a system of equations for the $\lambda_i$ and $\theta_k$, we proceed as follows:
For the current state $\{ x \; \lambda \; \theta \}$, calculate: the right hand side of the original system, $F(t, x)$; then matrix $Q^T \nabla F \; Q$ (which depends on the system state $x$ and on the $\theta_k$); the matrix $Q^T \dot{Q}$ (which depends on the $\theta_k$ and for which each entry is a linear function of the $\dot{\theta}_k$).
Equate the lower triangular entries of $Q^T \dot{Q}$ to the lower triangular entries of $Q^T \nabla F \; Q$ and solve the resulting linear system for the $\dot{\theta}_k$.
Equate the diagonal entries of $Q^T \nabla F \; Q$ with the derivatives $\dot{\lambda}_i$.
Step the current state forwards using the derivatives $\{ \dot{x} \; \dot{\lambda} \; \dot{\theta} \}$.
An example
Let us calculate the Lyapunov exponents of the driven van der Pol oscillator:
$$\dot{z}_1 = z_2$$ $$\dot{z}_2 = -d (1-z_1^2) z_2 - z_1 + b \cos \omega t$$ where $d$, $b$ and $\omega$ are real constants. For numerical calculations, we will use $d = -5$, $b = 5$ and $\omega = 2.466$. This (nonautonomous) system has chaotic orbits for this choice of parameters.
The gradient of the right hand side vector field for this system is
$$\nabla F = \begin{pmatrix} d_{11} & d_{12} \\ d_{21} & d_{22} \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 2 d z_1 z_2 - 1 & d(z_1^2 - 1) \end{pmatrix}.$$ The system is two-dimensional, so the orthogonal matrix $Q$ is characterised by a single angle $\theta_1$:
$$Q = \begin{pmatrix} \cos \theta_1 & -\sin \theta_1 \\ \sin \theta_1 & \cos \theta_1 \end{pmatrix}.$$ Then,
$$Q^T \dot{Q} = \begin{pmatrix} \cos \theta_1 & \sin \theta_1 \\ -\sin \theta_1 & \cos \theta_1 \end{pmatrix} \begin{pmatrix} -\sin \theta_1 & -\cos \theta_1 \\ \cos \theta_1 & -\sin \theta_1 \end{pmatrix} \dot{\theta}_1 = \begin{pmatrix} 0 & -\dot{\theta}_1 \\ \dot{\theta}_1 & 0 \end{pmatrix}$$ and the entries in the matrix $Q^T \nabla F \; Q$ are
$$(Q^T \nabla F \; Q)_{11} = d_{11} \cos^2 \theta_1 + (d_{12} + d_{21}) \sin \theta_1 \cos \theta_1 + d_{22} \sin^2 \theta_1,$$ $$(Q^T \nabla F \; Q)_{12} = d_{12} \cos^2 \theta_1 - (d_{11} - d_{22}) \sin \theta_1 \cos \theta_1 - d_{21} \sin^2 \theta_1,$$ $$(Q^T \nabla F \; Q)_{21} = d_{21} \cos^2 \theta_1 - (d_{11} - d_{22}) \sin \theta_1 \cos \theta_1 - d_{12} \sin^2 \theta_1,$$ $$(Q^T \nabla F \; Q)_{22} = d_{22} \cos^2 \theta_1 - (d_{12} + d_{21}) \sin \theta_1 \cos \theta_1 + d_{11} \sin^2 \theta_1.$$ Inserting explicit expressions for the entries of
$$\dot{z}_1 = z_2$$ $$\dot{z}_2 = -d (1-z_1^2) z_2 - z_1 + b \cos \omega t$$ $$\dot{\lambda}_1 = d z_1 z_2 \sin 2\theta_1 + d(z_1^2 - 1) \sin^2 \theta_1$$ $$\dot{\lambda}_2 = -d z_1 z_2 \sin 2\theta_1 + d(z_1^2 - 1) \cos^2 \theta_1$$ $$\dot{\theta}_1 = 2 d z_1 z_2 \cos^2 \theta_1 - 1 + d(z_1^2 - 1) \sin \theta_1 \cos \theta_1$$ This ODE system can be integrated using more or less any numerical scheme: here, we use the RKf45 scheme from the GSL library (via the Numeric.GSL.ODE module in the hmatrix Haskell package).
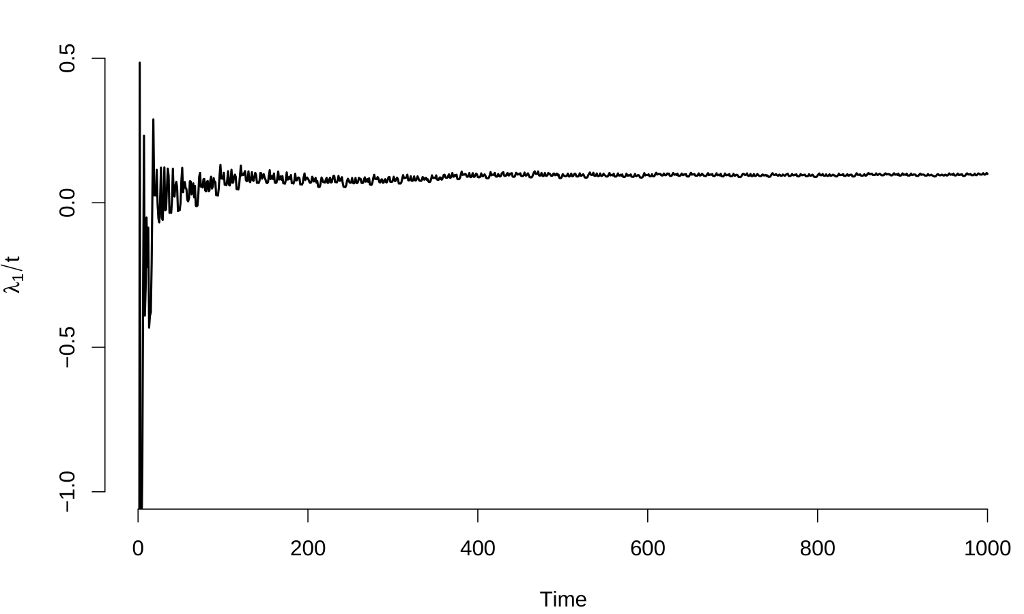
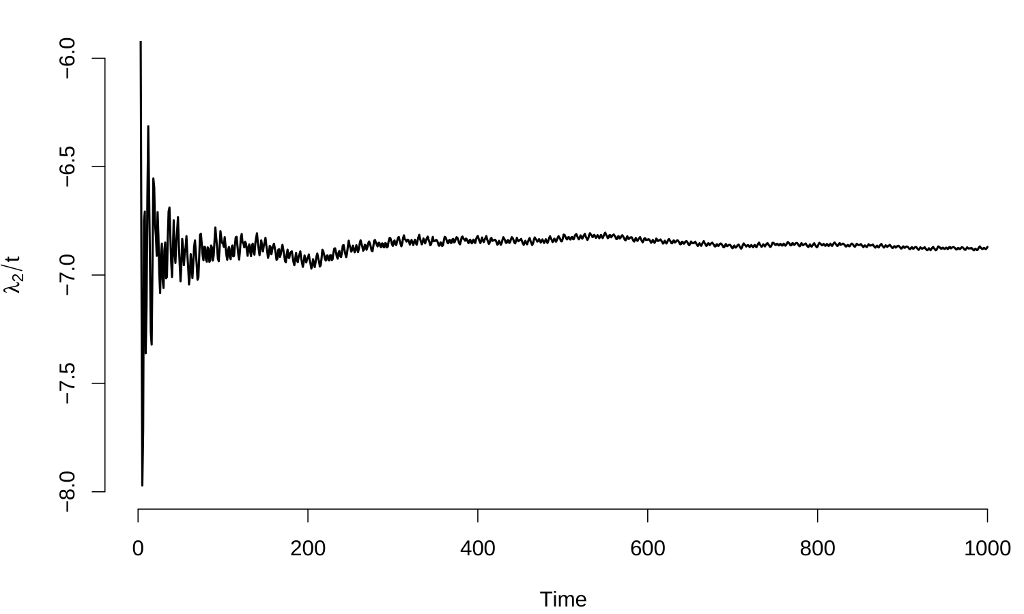
Here are plots of estimates of the Lyapunov exponents of this system generated using this approach:
We see rapid convergence of the estimates: taking the values in the time range [500, 1000], we estimate that the first Lyapunov exponent lies in the range [0.086601, 0.104736] and the second Lyapunov exponent in the range [-6.886599, -6.804369].
What next?
We want to implement this scheme for calculating Lyapunov exponents in Haskell. Questions that immediately arise:
How do we represent the input ODE system so that we can easily compute the gradient
$\nabla F$ ? Answer: as Haskell functions–we use automatic differentiation to evaluate the gradient efficiently.How can we manage the complexity of the $Q^T \dot{Q}$ matrix for larger systems? Answer: we use a semi-symbolic approach, where we evaluate and simplify the entries of $Q^T \dot{Q}$ once and use the result to build a matrix that allows us to extract the $\dot{\theta}_k$ derivatives.
How do we represent matrices and perform matrix computations? Answer: we use the
hmatrixpackage.
The next article in this series will present the code used to implement this scheme in Haskell, along with a slightly more complex example.