Lyapunov Exponents in Haskell: Part 2
In the previous article, we looked at some of the details of a scheme for calculating the Lyapunov exponents of a system of differential equations. In this post, we’ll see how to implement this scheme in Haskell. The code we describe is available as a Gist here.
Automatic differentiation
Given a dynamical system
$$\frac{dx}{dt} = F(t, x(t)),$$ one thing we need to do is calculate the gradient of $F$ for given values of $t$ and $x$. We can do this most easily using automatic differentiation, a method that allows us to calculate derivatives of functions to machine precision without using finite differences. There are a number of Haskell libraries that provide automatic differentiation facilities, but we’ll use Edward Kmett’s ad package. The only thing we need is the jacobian function from the Numeric.AD module. Using this, we calculate the right hand side of our “basic equation”, $Q^T \nabla F \; Q$, using the function
rhs :: (forall s. Mode s => AD s Double -> [AD s Double] -> [AD s Double]) -> Double -> State -> Matrix Double rhs f t (State x lams ths) = (trans q) <> jac <> q where q = evalRot (rot n) ths jac = fromLists $ jacobian (f $ lift t) (toList x) n = dim x
Here, the function rot calculates a simplified symbolic representation of the $n$-dimensional rotation matrix $Q$ and evalRot evaluates this symbolic representation for given numeric values of the angle variables.
The beauty of the automatic differentiation approach is that we are able to provide the functions defining the right hand side of the dynamical system we want to analyse as normal Haskell functions. The only slight downside is that we need to use rank-2 types to be able to express the type of the input functions correctly: the automatic differentiation approach works by evaluating these functions at a different type than the Double -> [Double] -> [Double] type we would use for straightforward numerical integration of the dynamical system, and we need to carry that generality in the type of the first parameter of the rhs function.
The State type is a simple record that carries around the state of the underlying dynamical system along our reference trajectory, plus the $\lambda_i(t)$ and $\theta_k(t)$:
data State = State { x :: Vector Double , lams :: Vector Double , ths :: Vector Double } deriving (Eq, Show)
There is a little bit of back-and-forth between list and Matrix representations to accommodate the requirements of the ad package, but we mostly try to work in terms of the hmatrix Vector and Matrix types, at least as long as we’re dealing with numeric values.
Representing rotation matrices
Much of what we need to do is tied up with how we represent the $Q$ matrix and how we simplify the $Q^T \dot{Q}$ expression that appears on the left hand side of our basic equation. We use a simplified symbolic representation of these matrices to allow us to simplify them once and for all before we start using them at every step of our numerical integration. The algebraic forms of $Q$ and $Q^T \dot{Q}$ are identical for all systems of the same size, and the $Q^T \dot{Q}$ rapidly becomes quite complicated for larger $n$, so it’s worth dealing with this complexity up front.
Basic expression types
Entries in $Q$ and $Q^T \dot{Q}$ in general consist of sums of terms involving an integer coefficient and products of sines and cosines of the $\theta_k$ and (for $Q^T \dot{Q}$) a single time derivative of one of the $\theta_k$. We represent these expressions using some simple types. (We define Show instances for all of these for debugging, but I won’t show the code for those here.) First, simple factors, which are either $\cos \theta_k$ (C k), $\sin \theta_k$ (S k) or $\dot{\theta}_k$ (D k):
data Factor = Null | C Int | S Int | D Int deriving (Eq, Ord)
Then, terms are products of factors, with an integer coefficient:
data Term = Term { coef :: Integer, facs :: [Factor] } deriving (Eq)
Finally, expressions are sums of terms:
newtype Expr = Expr [Term] deriving (Eq, Ord)
We define multiplication of terms in the obvious kind of way (maintaining factors in a canonical sorted order):
fmult :: Term -> Term -> Term fmult (Term c1 fs1) (Term c2 fs2) = Term (c1 * c2) (L.sort $ fs1 ++ fs2)
and then we have a Num instance for expressions which, apart from expression simplification, is pretty self-explanatory:
instance Num Expr where fromInteger n = Expr [Term n []] negate (Expr ts) = Expr $ map (\(Term c fs) -> Term (-c) fs) ts (Expr ts1) + (Expr ts2) = simplify $ Expr $ L.sort (ts1 ++ ts2) (Expr ts1) * (Expr ts2) = simplify $ Expr $ L.sort [fmult t1 t2 | t1 <- ts1, t2 <- ts2] signum _ = error "signum not appropriate for Expr" abs _ = error "abs not appropriate for Expr"
And we have a few small helper functions for creating elementary expressions:
c, s, d :: Int -> Expr c i = Expr [Term 1 [C i]] s i = Expr [Term 1 [S i]] d i = Expr [Term 1 [D i]]
Simplification of expressions
When we construct the $Q^T \dot{Q}$ matrix below, the expressions involving the $\theta_k$ become quite complicated, and it makes sense to simplify as far as possible. Because of the structure of the entries in this matrix, we can restrict the simplifications performed to removal of zero terms, merging of terms involving identical factors, and (the most complex) simplification of trignometric sums using the identity $\cos^2 \theta + \sin^2 \theta = 1$. Simplification is repeated, using these three steps, until no further changes can be made:
simplify :: Expr -> Expr simplify (Expr ts) = Expr $ firstFix (iterate step ts) where firstFix (x1:x2:xs) | x1 == x2 = x1 | otherwise = firstFix (x2:xs) step = dropZeros . mt . trig dropZeros = filter ((/=0) . coef) mt [] = [] -- Term merging. mt [t] = [t] mt (t1:(t2:ts)) | facs t1 == facs t2 = mt $ (Term (coef t1 + coef t2) (facs t1)):ts | otherwise = t1 : (mt $ t2:ts)
The most complex simplification step is the reduction of sums of terms, one involving $\cos^2 \theta_k$ and the other $\sin^2 \theta_k$. We only do one simplification step here, since simplify repeats simplification steps until we reach a fixed point. The approach is pretty brute force, simply searching for a pair of matching terms (i.e. two terms with identical factors except that one term has a $\cos^2 \theta_k$ factor and the other a $\sin^2 \theta_k$ factor) and merging them.
trig ts = go ts where go [] = [] go (t:ts) | null reps = t : go ts | otherwise = case match reps t ts of Nothing -> t : go ts Just (f, mt, ts') -> combine f t mt ++ ts' where reps = repeats t -- Find repeated factors (i.e. cos^2 or sin^2) in a term. repeats (Term _ fs) = map head . filter ((>1) . length) $ L.group fs -- Match repeated factors in a term against repeated factors -- in following terms. match [] m ts = Nothing match (f:fs) m ts = case matchOne f m ts of Nothing -> match fs m ts Just (f, mt) -> Just (f, mt, L.delete mt ts) -- Match a single repeated factor against following terms. matchOne f m [] = Nothing matchOne f m (t:ts) | matchFac f `elem` repeats t && filter (/=f) (facs m) == filter (/=matchFac f) (facs t) && signum (coef m) == signum (coef t) = Just (f, t) | otherwise = matchOne f m ts -- cos^2 can be paired off with sin^2, and vice versa. matchFac (C x) = S x matchFac (S x) = C x -- Combine terms with compatible repeated elements. combine f (Term c1 fs1) (Term c2 fs2) = case compare c1 c2 of EQ -> [Term c1 fs1'] LT -> [Term c1 fs1', Term (c2-c1) fs2] GT -> [Term c2 fs2', Term (c1-c2) fs1] where fs1' = L.delete f $ L.delete f fs1 fs2' = L.delete mf $ L.delete mf fs2 mf = matchFac f
Other expression manipulations
As well as the operations implemented by the Num instance for Expr, we also need to be able to differentiate expressions, which we do symbolically using the product rule and Leibnitz’s rule:
diff :: Expr -> Expr diff (Expr ts) = L.foldl1' (+) $ map diffTerm ts where diffTerm (Term c fs) = L.foldl1' (+) $ map single $ zipWith fmult des leaveOneOuts where des = map diffFac fs leaveOneOuts = map (Term c) [take n fs ++ drop (n + 1) fs | n <- [0..length fs - 1]] single t = Expr [t] diffFac (D _) = error "No second derivatives!" diffFac (S pos) = Term 1 [C pos, D pos] diffFac (C pos) = Term (-1) [S pos, D pos]
and we also need to be able to find the numerical value of an expression given values for the $\theta_k$:
eval :: (Vector Double, Vector Double) -> Expr -> Double eval (ctheta, stheta) (Expr ts) = sum $ map evalTerm ts where evalTerm (Term c fs) = fromInteger c * (product $ map evalFactor fs) evalFactor (C i) = ctheta @> (i-1) evalFactor (S i) = stheta @> (i-1) evalFactor _ = error "Can't evaluate this factor!"
Expression matrices
All the definitions above deal with individual expressions, but most of what we want to do involves matrices of expressions. We use a simple list representation for these matrices since none of them will be very large. We call this type Mat to avoid conflicts with hmatrix types. We use this type only for our symbolic manipulations to build the $T(\theta)$ matrix used to calculate the $\dot{\theta}_k$.
newtype Mat a = Mat [[a]] deriving (Eq)
We define a Functor instance for Mat and a few basic matrix operations: transpose, dot products, and matrix multiplication (represented by the operator %*%):
instance Functor Mat where fmap f (Mat xs) = Mat $ map (map f) xs transpose :: Mat a -> Mat a transpose (Mat xs) = Mat (L.transpose xs) dot :: Num a => [a] -> [a] -> a dot v1 v2 = sum $ zipWith (*) v1 v2 (%*%) :: Num a => Mat a -> Mat a -> Mat a (Mat m1) %*% (Mat m2) = Mat [[r `dot` c | c <- L.transpose m2] | r <- m1]
Rotation matrices
Given the above definitions, representing elementary rotation matrices (Givens rotations) is simple. The arguments to the elemRot function are the system dimension n and a tuple ((i,j),k) giving the indices of the rotation, i.e. saying which $\theta_{ij} = \theta_k$ is being used, and hence which two axes are involved in the 2-dimensional elementary rotation.
elemRot :: Int -> ((Int,Int),Int) -> Mat Expr elemRot n ((i,j),idx) = Mat [[entry (k,l) | l <- [1..n]] | k <- [1..n]] where entry (k,l) | k == l && k /= i && k /= j = 1 | k == l && (k == i || k == j) = c idx | k == i && l == j = s idx | k == j && l == i = -s idx | otherwise = 0
The full rotation matrix for dimension n is then generated by
rot :: Int -> Mat Expr rot = memo rot' where rot' n = L.foldl1' (%*%) $ map (elemRot n) (idxs n)
We memoize the result of this function (using the MemoTrie package, but any other memoizing approach would work) to prevent recalculation of these potentially complicated values. We need an ordering of the matrices, which we generate using the idxs function. Throughout the code, we need to refer to elements of the lower-triangular part of matrices (all the matrices we deal with are either symmetric or skew-symmetric, so we deal with the diagonal and the lower triangular elements separately). For an $n \times n$ matrix, there are $n(n-1)/2$ elements in the lower-triangular part, which we label with integers $1 \dots n(n-1)/2$ in the order given here:
idxs :: Int -> [((Int,Int),Int)] idxs n = zip [(j, i) | i <- [1..n], j <- [2..n], i < j] [1..]
Given a matrix of expressions, we also provide a convenience function to convert from expression form to numeric values by passing in vector of angles:
evalRot :: Mat Expr -> Vector Double -> Matrix Double evalRot q theta = fromLists matrep where Mat matrep = fmap (eval cstheta) q cstheta = (mapVector cos theta, mapVector sin theta)
Dealing with the left hand side
Given the above matrix and expression types, we can easily calculate a symbolic representation of $Q^T \dot{Q}$:
qtqdot :: Int -> Mat Expr qtqdot n = (transpose q) %*% (fmap diff q) where q = rot n
We can test this in GHCi:
Prelude> :load lyapunov.hs [1 of 1] Compiling LyapunovExponents ( lyapunov.hs, interpreted ) Ok, modules loaded: LyapunovExponents. *LyapunovExponents> qtqdot 2 [0,-D1] [D1,0]
showing that for a 2-dimensional system,
$$Q^T \dot{Q} = \begin{pmatrix} 0 & -\dot{\theta}_1 \\ \dot{\theta}_1 & 0 \end{pmatrix}$$
*LyapunovExponents> qtqdot 3 [0,-C2 C3 D1 - S3 D2,C2 S3 D1 - C3 D2] [C2 C3 D1 + S3 D2,0,-S2 D1 - D3] [-C2 S3 D1 + C3 D2,S2 D1 + D3,0]
so that for a 3-dimensional system,
$$Q^T \dot{Q} = \begin{pmatrix} 0 & -\cos \theta_2 \cos \theta_3 \dot{\theta}_1 - \sin \theta_3 \dot{\theta}_2 & \cos \theta_2 \sin \theta_3 \dot{\theta}_1 - \cos \theta_3 \dot{\theta}_2 \\ \cos \theta_2 \cos \theta_3 \dot{\theta}_1 + \sin \theta_3 \dot{\theta}_2 & 0 & -\sin \theta_2 \dot{\theta}_1 - \dot{\theta}_3 \\ -\cos \theta_2 \sin \theta_3 \dot{\theta}_1 + \cos \theta_3 \dot{\theta}_2 & \sin \theta_2 \dot{\theta}_1 + \dot{\theta}_3 & 0 \end{pmatrix}$$
and finally, just to demonstrate the increasing complexity of $Q^T \dot{Q}$ as $n$ gets larger:
*LyapunovExponents> qtqdot 4
[0,-S5 D3 - C3 C5 S4 D2 - C2 C3 C4 C5 D1,-C3 C4 C6 D2 + C2 C3 C6 S4 D1 - C5 S6 D3
+ C3 S4 S5 S6 D2 + C2 C3 C4 S5 S6 D1,C3 C4 S6 D2 - C2 C3 S4 S6 D1 - C5 C6 D3
+ C3 C6 S4 S5 D2 + C2 C3 C4 C6 S5 D1]
[S5 D3 + C3 C5 S4 D2 + C2 C3 C4 C5 D1,0,-C5 C6 D4 - S6 D5 - C5 C6 S2 D1 - C5 C6 S5 D6
- S3 S4 S6 D2 - C2 C4 S3 S6 D1 + C4 C6 S3 S5 D2 - C2 C6 S3 S4 S5 D1 + C5 C6 S5 D6,
C5 S6 D4 - C6 D5 + C5 S2 S6 D1 + C5 S5 S6 D6 - C6 S3 S4 D2 - C2 C4 C6 S3 D1
- C4 S3 S5 S6 D2 + C2 S3 S4 S5 S6 D1 - C5 S5 S6 D6]
[C3 C4 C6 D2 - C2 C3 C6 S4 D1 + C5 S6 D3 - C3 S4 S5 S6 D2 - C2 C3 C4 S5 S6 D1,
C5 C6 D4 + C5 C6 S2 D1 + S3 S4 S6 D2 + S6 D5 + C2 C4 S3 S6 D1 - C4 C6 S3 S5 D2
+ C2 C6 S3 S4 S5 D1,-C6 S6 D6 + C5 S5 S6 S6 D5 + C6 S6 D6 - C5 S5 S6 S6 D5,
-S5 D4 - D6 - S2 S5 D1 - C4 C5 S3 D2 + C2 C5 S3 S4 D1]
[-C3 C4 S6 D2 + C2 C3 S4 S6 D1 + C5 C6 D3 - C3 C6 S4 S5 D2 - C2 C3 C4 C6 S5 D1,
-C5 S6 D4 - C5 S2 S6 D1 + C6 S3 S4 D2 + C6 D5 + C2 C4 C6 S3 D1 + C4 S3 S5 S6 D2
- C2 S3 S4 S5 S6 D1,S5 D4 + S2 S5 D1 + D6 + C4 C5 S3 D2 - C2 C5 S3 S4 D1,
C6 S6 D6 + C5 C6 C6 S5 D5 - C6 S6 D6 - C5 C6 C6 S5 D5]In order to extract explicit values for the $\dot{\theta}_k$, we need to construct the matrix $T(\theta)$, such that $T(\theta) \dot{\theta} = L$, where $L$ is a vector of the lower triangular entries of $Q^T \nabla F \; Q$ in the order defined by the idxs function. The $T$ matrix is calculated by the following (memoized) function:
tMatrix :: Int -> Mat Expr tMatrix = memo tMatrix' where tMatrix' n = Mat $ map makeRow es where es = qtqdotEntries n makeRow (Expr ts) = map (makeEntry ts) [1..size] makeEntry ts i = Expr . map (deleteD i) . filter (hasD i) $ ts size = n * (n-1) `div` 2 hasD i (Term _ fs) = (D i) `elem` fs deleteD i (Term c fs) = Term c $ L.delete (D i) fs
and we find:
*LyapunovExponents> tMatrix 2 [1] *LyapunovExponents> tMatrix 3 [C2 C3,S3,0] [-C2 S3,C3,0] [S2,0,1] *LyapunovExponents> tMatrix 4 [C2 C3 C4 C5,C3 C5 S4,S5,0,0,0] [-C2 C3 C6 S4 - C2 C3 C4 S5 S6,C3 C4 C6 - C3 S4 S5 S6,C5 S6,0,0,0] [C5 C6 S2 + C2 C4 S3 S6 + C2 C6 S3 S4 S5,S3 S4 S6 - C4 C6 S3 S5,0,C5 C6,S6,0] [C2 C3 S4 S6 - C2 C3 C4 C6 S5,-C3 C4 S6 - C3 C6 S4 S5,C5 C6,0,0,0] [-C5 S2 S6 + C2 C4 C6 S3 - C2 S3 S4 S5 S6,C6 S3 S4 + C4 S3 S5 S6,0,-C5 S6,C6,0] [S2 S5 - C2 C5 S3 S4,C4 C5 S3,0,S5,0,1]
For the code as presented here, compiled with optimisation on using GHC, calculating the $10 \times 10$ $T(\theta)$ for a 5-dimensional system takes a bit more than 2 minutes using a single core on my machine. There is reason to believe that it might still be practical to use this method for larger systems though–I’ve made no attempt at all to make my symbolic computations efficient, and it might be possible to develop some sort of recurrence relation directly relating $T(\theta)$ for an $n+1$-dimensional system to $T(\theta)$ for an $n$-dimensional system, which would make the computation of $T$ quicker. (We can also build reduced systems for evaluating a subset of the Lyapunov spectrum: more on this in a later article, if I can get it to work!)
Putting things together
Given the above elements, we can now write a function that computes the full right hand side derivative for numerical integration of the state of our dynamical system supplemented with the $\lambda_i$ and $\theta_k$. We calculate $\dot{x}$ for the main system state using the function f passed in, then calculate the right hand side of our “basic equation”, $Q^T \nabla F \; Q$ using the rhs function. The $\dot{\lambda}_i$ are the diagonal entries of this matrix. Finally, extracting the lower triangular entries from $Q^T \nabla F \; Q$ and building the $T(\theta)$ matrix allows us to determine the $\dot{\theta}_k$.
fullRhs :: (forall t. Floating t => t -> [t] -> [t]) -> Double -> State -> Vector Double fullRhs f t s@(State x lams ths) = join [xdot, lamdot, thdot] where n = dim x -- Time derivative from original system. xdot = fromList . f t . toList $ x -- RHS of evolution equation for fundamental solution matrix. r = rhs f t s -- Time derivatives for scaled LEs. lamdot = takeDiag r -- T(\theta) for current \theta values. tm = evalRot (tMatrix n) ths -- Lower triangular entries from the RHS of the evolution -- equation for the fundamental solution matrix, corresponding -- to \dot{\theta} entries. tmrhs = fromList [r @@> (i-1,j-1) | ((i,j),_) <- idxs n] -- Solve for \dot{\theta} using T(\theta) and the lower -- triangular part of r. thdot = tm <\> tmrhs
We then need a couple of helper functions to help interface with the ODE solvers in the Numeric.GSL.ODE package:
stateFromList :: [Double] -> State stateFromList lx = State (fromList x) (fromList lam) (fromList th) where (x,lamth) = splitAt n lx (lam,th) = splitAt n lamth n = isqrt (9 + 8 * length lx) - 3 `div` 2 isqrt = floor . sqrt . fromIntegral stateToList :: State -> [Double] stateToList (State x lam th) = concat [toList x, toList lam, toList th] odeSolveRhs :: (forall t. Floating t => t -> [t] -> [t]) -> (Double -> [Double] -> [Double]) odeSolveRhs sf t lx = toList $ fullRhs sf t (stateFromList lx)
and we’re ready to go with the main public interface to the code:
lyapunov :: (forall t. Floating t => t -> [t] -> [t]) -> State -> Vector Double -> (State, Matrix Double) lyapunov f istate ts = (fstate, fromColumns $ ts : cols) where odef = odeSolveRhs f soln = odeSolve odef (stateToList istate) ts cols = zipWith ($) fs (toColumns soln) fs = replicate n id ++ replicate n (`divide` ts) ++ replicate (n * (n - 1) `div` 2) id n = dim (x istate) fstate = stateFromList . toList . last . toRows $ soln
Called with a function f, an initial state for the full system (produced by the initialState function) and a vector of time values, this produces as output a matrix with the time values in the first column, the values of the variables of the ODE system in the next $n$ columns, estimates for the Lyapunov exponents of the system in the next $n$ columns and the values of the angles $\theta_k$ in the last $n(n-1)/2$ columns.
Two examples
The driven van der Pol oscillator
Let’s first look at the same system as we treated by hand in the previous post:
$$\dot{z}_1 = z_2$$ $$\dot{z}_2 = -d (1-z_1^2) z_2 - z_1 + b \cos \omega t$$ with $d$, $b$ and $\omega$ are real constants. As before, we will put $d = -5$, $b = 5$ and $\omega = 2.466$. In Haskell:
module VDP where import Data.Default data VdpParam t = VdpParam { d :: t, b :: t, omega :: t } deriving (Eq, Show) instance Floating t => Default (VdpParam t) where def = VdpParam (-5) 5 2.466 vdp :: Floating t => t -> [t] -> [t] vdp = vdpWith def vdpWith :: Floating t => VdpParam t -> t -> [t] -> [t] vdpWith (VdpParam d b omega) t [z1,z2] = [dz1,dz2] where dz1 = z2 dz2 = -d * (1 - z1**2) * z2 - z1 + b * cos (omega * t)
One would then hope that we could type something like the following in GHCi to see an estimate for the first Lyapunov exponent of the system:
GHCi, version 7.4.2: http://www.haskell.org/ghc/ :? for help ...> :load VDP.hs Numeric/LyapunovExponents.hs ...> :m + Numeric.LyapunovExponents Numeric.LinearAlgebra ...> let ic = initialState [1,1] ...> let ts = linspace 1001 (0,100) :: Vector Double ...> let soln = lyapunov vdp ic ts ...> (snd soln) @@> (1001,4) Bus error
Oops. This may work on a 32-bit system (I’ve not tried it), but on a 64-bit system, you will get bitten by this bug. It’s likely to be fixed in GHC 7.8.1, but it’s kind of a nasty thing to have to deal with, so it’s no surprise that it’s been punted a few times.
It’s only a problem in GHCi though, not the GHC compiler, so we can avoid the problem by compiling a little program like this:
import Numeric.LyapunovExponents import Numeric.LinearAlgebra import VDP ic :: State ic = initialState [1,1] ts :: Vector Double ts = linspace 1001 (0,1000) soln :: Matrix Double soln = snd $ lyapunov vdp ic ts main = saveMatrix "vdp.dat" "%f" $ (fromLists . tail . toLists) soln
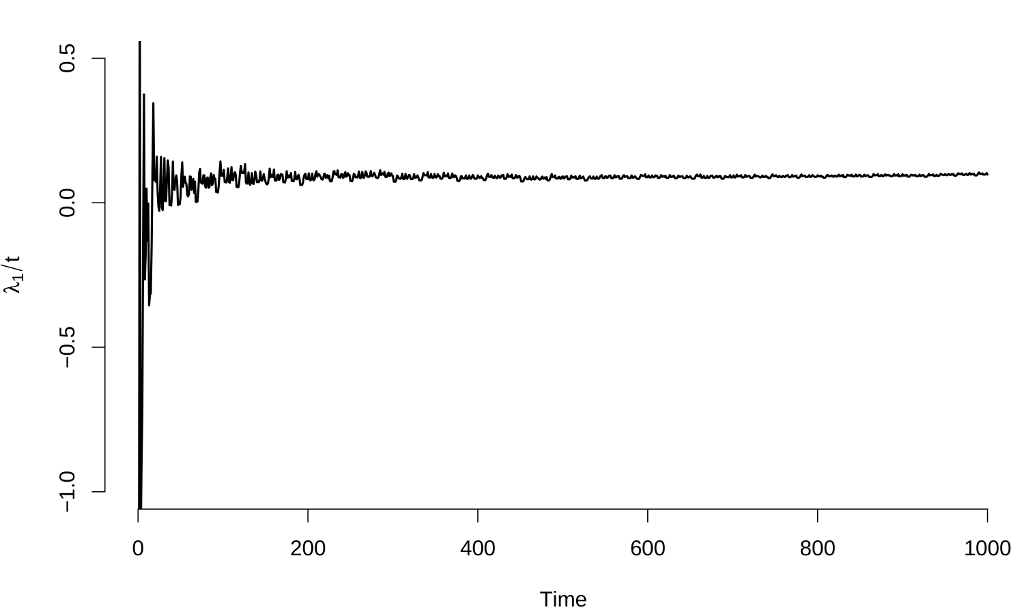
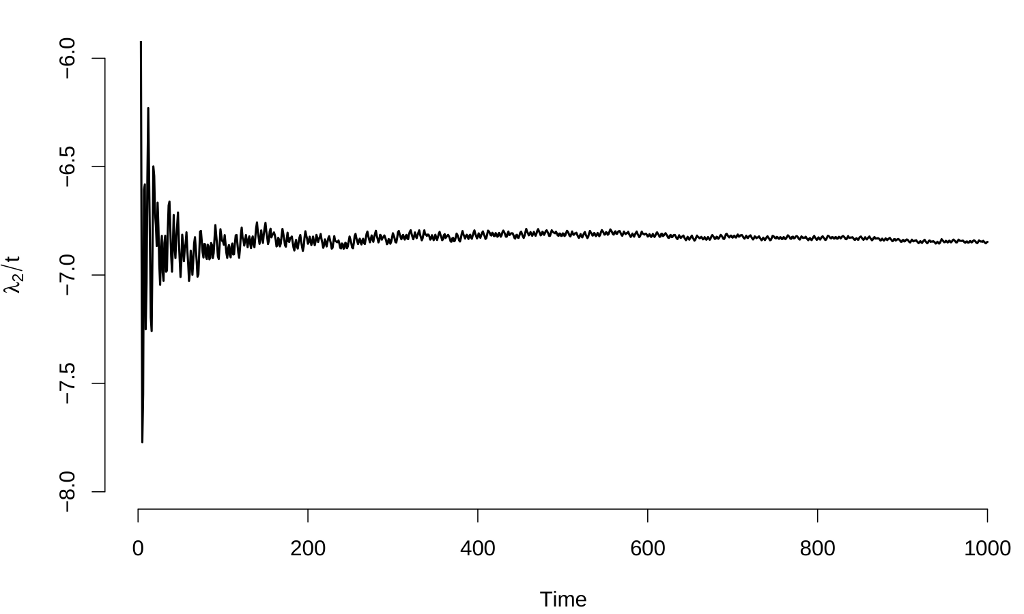
Compiling and running this works fine, and here are graphs of the Lyapunov exponent estimates:
These results are identical to those from the manual calculation in the previous post ($\lambda_1 \approx 0.092 \pm 0.005$, $\lambda_2 \approx -6.828 \pm 0.013$), values which agree with other calculations in the literatureFor example, S. Habib and R. D. Ryne, Phys. Rev. Lett. 74, 70 (1995)..
The Lorenz system
Next, let’s look at the Lorenz system
$$\frac{dx}{dt} = \sigma (y - x)$$ $$\frac{dy}{dt} = x (\rho - z) - y$$ $$\frac{dz}{dt} = x y - \beta z$$ with the “traditional” parameter choices $\sigma = 10$, $r = 28$ and $b = 8/3$. The Haskell representation of this system is:
module Lorenz where import Data.Default data LzParam t = LzParam { sigma :: t, r :: t, b :: t } deriving (Eq, Show) instance Floating t => Default (LzParam t) where def = LzParam 10 28 (8/3) lorenz :: Floating t => t -> [t] -> [t] lorenz = lorenzWith def lorenzWith :: Floating t => LzParam t -> t -> [t] -> [t] lorenzWith (LzParam sigma r b) _ [x, y, z] = [sigma * (y - x) , r * x - y - x * z , x * y - b * z]
and, as before, we use a little freestanding program to integrate the equations governing the Lyapunov exponents to get around the GHCi bug:
import Numeric.LyapunovExponents import Numeric.LinearAlgebra import Lorenz ic :: State ic = initialState [1,1,1] ts :: Vector Double ts = linspace 10001 (0,1000) soln :: Matrix Double soln = snd $ lyapunov lorenz ic ts main = saveMatrix "lorenz.dat" "%f" $ (fromLists . tail . toLists) soln
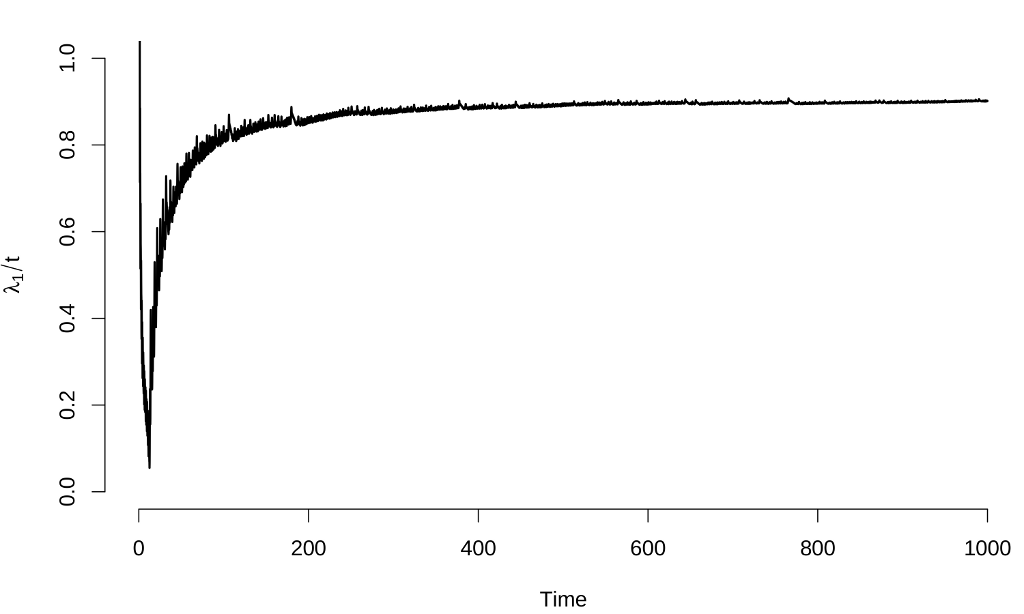
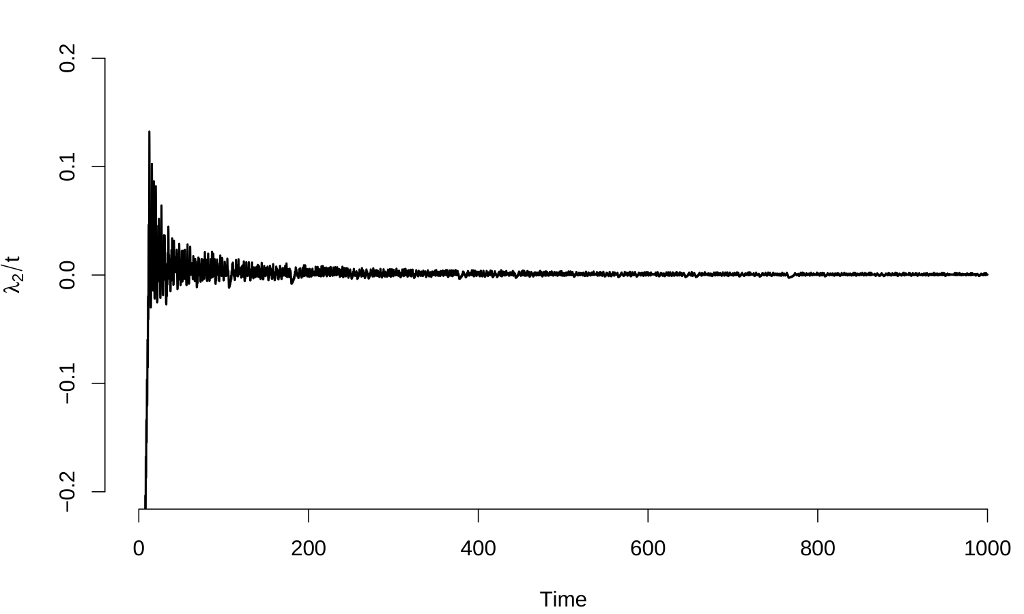
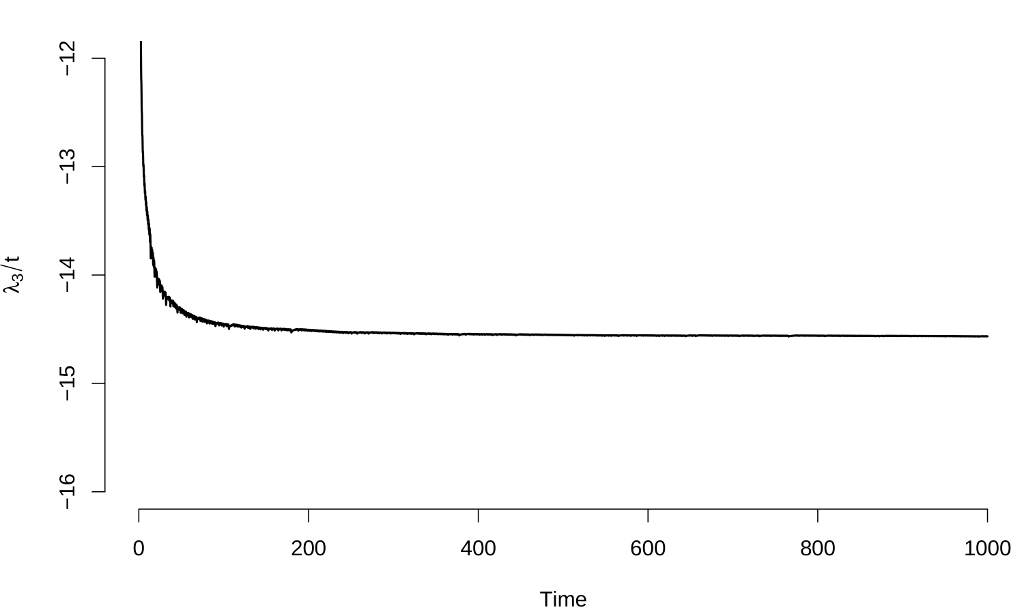
Here are the results:
The estimates of the Lyapunov exponents are $\lambda_1 \approx 0.897 \pm 0.003$, $\lambda_2 \approx 0.000 \pm 0.001$ and $\lambda_3 \approx -14.560 \pm 0.003$, results that again are consistent with other calculation methods.
Some comments
The code presented here is no more than a proof of concept:
The symbolic calculations are not done in a particularly efficient way, and we might hope, in particular, to do a much better job of calculating the entries in the $Q^T \dot{Q}$ matrix that we need for determining the $\dot{\theta}_k$–at least by memoizing these calculations, they only get done once;
We have no way of calculating only a subset of the Lyapunov spectrum, which should be possible using this method, and is the only practical way to proceed for larger systems;
We have glossed over some important technical issues, including the question of whether the $T(\theta)$ matrix is always nonsingular–in general, this is a complicated question and there are more sophisticated schemes that exist to ensure that our approach remains well-founded: for now, we just trust to luck;
We need to calculate the Jacobian $\nabla F$ in full, which is impractical for larger systems, meaning that we might want to try to use some sort of matrix-free method (this is tricky, but is worth it for larger systems: even for the small systems considered here, a large fraction of the compute time goes into evaluations of $\nabla F$).
Given all those caveats, the code works (although it’s slow), and was pretty straightforward to write in Haskell. Haskell really is nice for symbolic calculations, and the ability to implement things like automatic differentiation directly in the language itself is a real plus.