Data visualisation
I’ve been interested in scientific data visualisation for a long time. It takes a lot of effort to produce effective visualisations that get across the most important message in the data and at the same time are visually pleasing. Here are a selection of images I’ve produced for various different purposes. Click on any of the images for a larger version.
I’ve used a lot of different data visualisation tools: my current main toolbox includes NCAR’s NCL, R and POV-Ray.
“Standard” plots
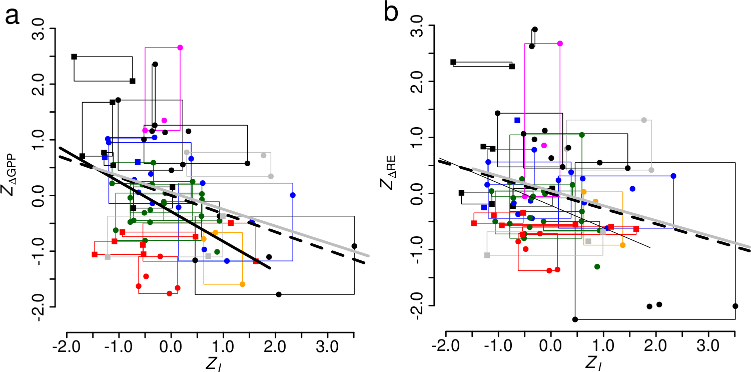
When I say “standard” plots, I mean the kind of thing that you can see in more or less any journal article: regression plots, simple maps, contour plots, and so on. Of course, even the most standard of standard plots can be enhanced by small extras. This plot is a simple regression plot (for this paper) showing the relationship between standardised scores of precipitation intensity and ecosystem fluxes (GPP, gross primary productivity and RE, ecosystem respiration), all taken from the FLUXNET data set, after taking into account ecosystem flux variations caused by variations in total rainfall amount. The data set I used consists of data for multiple sites, with different numbers of data years for each site. Each point on each plot shows the results for a single site-year, coloured according to the ecosystem type of the site, and using different symbols for predominantly dry sites and predominantly wet sites. The grey and black lines show linear regressions at different levels of significance (line width) and different data subsets (line colour and style). So far, so standard. The main extra feature here is the boxes, which encompass the range of variability of values seen for each site (i.e., there is one box per site). This gives an immediate visual representation of the range of intra-site variability (caused by differences from year to year at the same site) and inter-site variability (caused by intrinsic differences between sites).
Another example is this composite image (from this paper), which shows, for the LPJ-WHyMe permafrost vegetation model, the sensitivity of three important soil parameters (soil temperature at 25 cm depth, active layer depth, ALD, and water table position, WTP) to changes in climatic conditions. The top panel shows temperature changes for the boreal regions projected from an IPCC SRES scenario, while the lower panels show the results of sensitivity experiments for the six points indicated. The sensitivity experiments varied air temperature and precipitation independently across a range of values comparable to changes predicted from IPCC scenarios. The black dots in each of the lower panel show the conditions projected at each test site from the IPCC scenario used to produce the upper panel map and the dashed lines an indicative trajectory that each site might follow to reach the conditions in the IPCC scenario.
The principal idea with all of these plots is to display the maximal amount of information in the clearest way possible. In many cases, this is done by carefully adding extra elements to standard plots, or compositing multiple parallel standard plots to allow comparison between different variables or different conditions.
In some cases, it can be better to invent a new kind of plot, not quite fitting into the standard categories. This plot shows an example. It’s very common in modelling studies that we perform parameter sensitivity experiments, to try to determine which parameters in our models are most influential. With several parameters and several model outputs to consider, the amount of data produced by such sensitivity experiments can be large. Here, we consider methane fluxes simulated by a permafrost vegetation methane emission model. We have four types of fluxes (total, plant-mediated, diffusion and ebullition), we are interested in the effects of varying seven different parameters, and we consider seven representative sites (numbers 1–7). This leads to a lot of model output. We can visualise the effect of varying different model parameters by considering linear regressions between model outputs (methane fluxes) and parameter values. Here, we display both the regression slope (using colour) and the correlation coefficient (using the size of the blobs) for all of these relationships. The most important relationships (big blobs, saturated colours) jump right out at you. Detecting which are the important parameters in a page-full of normal regression plots is much more difficult.
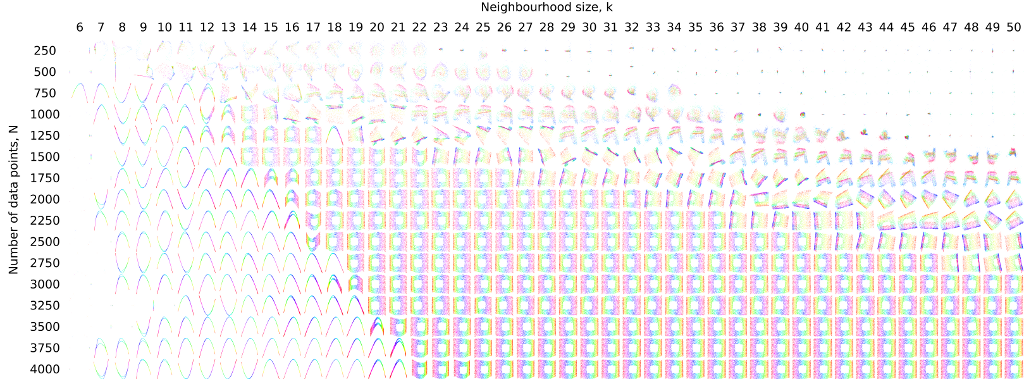
Another way to display large amounts of information in a comprehensible way is to follow Ed Tufte’s “small multiples” principle. Below is an extreme example. These images show sensitivity tests for a nonlinear dimensionality reduction method called Hessian locally linear embedding (HLLE) on a simple geometric test data set. The test data is a cloud of three-dimensional points (labelled by colour) representing a rectangular strip rolled up into a “Swiss roll” with a square hole in the middle. The HLLE method aims to recover the intrinsic two-dimensional structure of the dataset from the 3-dimensional point cloud–a good result in the images below is a square with a square hole, with the points arranged in “rainbow” order from one end of the square to the other, with as little distortion of the square as possible. The “small multiples” show the results of running the HLLE algorithm for different numbers of data points (vertical axis) and different values of a neighbourhood size parameter used by the algorithm (horizontal axis). The left-hand image shows the results with perfect data (no noise) and the right-hand image with a small amount of Gaussian noise added to the positions of the points in the 3-dimensional point cloud. Without going into details (if you’re interested, you can read this blog post or if you’re feeling particularly masochistic, Chapter 8 of my PhD thesis), it’s clear from the overview that the small multiples approach gives that there are systematic variations in the performance of the HLLE algorithm as the number of data points and the neighbourhood size vary, and that there are clear differences between the behaviour with and without noise in the data. All of these features can be explained relatively straightforwardly, but the immediate visual impact of these figures is quite striking.
“Cartoon” plots
The “small multiples” method works well when you have lots of data of the same type to display, but if you have several different kinds of data that you want to show on the same image, you need to be a little more creative. The examples here arose from a need to plot results from a permafrost vegetation model: we had monthly annual cycles of soil temperature (as depth profiles), water table position (as well as information about standing surface water or snow cover) and vegetation productivity for a number of vegetation types. We could have tried to produce some sort of horrible line graph displaying all this information, but when we saw this image in one of Tufte’s books, we had a better idea. For each month, the images below show a soil profile, which is either brown (dry), blue (water saturated) or grey (frozen), with a temperature profile superimposed. Standing water and/or snow cover is shown above the soil surface, and bars above the soil surface show vegetation productivity for five selected vegetation types. This visualisation provides a direct view of the active layer dynamics (the layer of soil that isn’t permanently frozen), vital for the timing of vegetation growth in boreal regions.
The images are SVG files (so your browser may not display them correctly–Internet Explorer, in particular, has poor or non-existent SVG support), created programmatically using a Perl script that reads in the annual cycle of data values and renders each monthly profile accordingly. It’s hard to imagine creating these visualisations in a “standard” tool, and drawing them by hand would be extremely laborious and error-prone. It’s a shame that images like this are so difficult to produce, since they are extremely effective.
Ray-tracing with POV-Ray
Sometimes, you want something a bit more visually polished. I started using the POV-Ray ray tracer to produce images for posters and proposals, since it’s possible to make very slick graphics with relatively little effort. I say “relatively” because it can still be quite a bit of work to produce the geometry for the ray tracer from whatever data you want to represent: this is the same idea as the programmatic generation of SVG images from data presented above, but rather more complex.
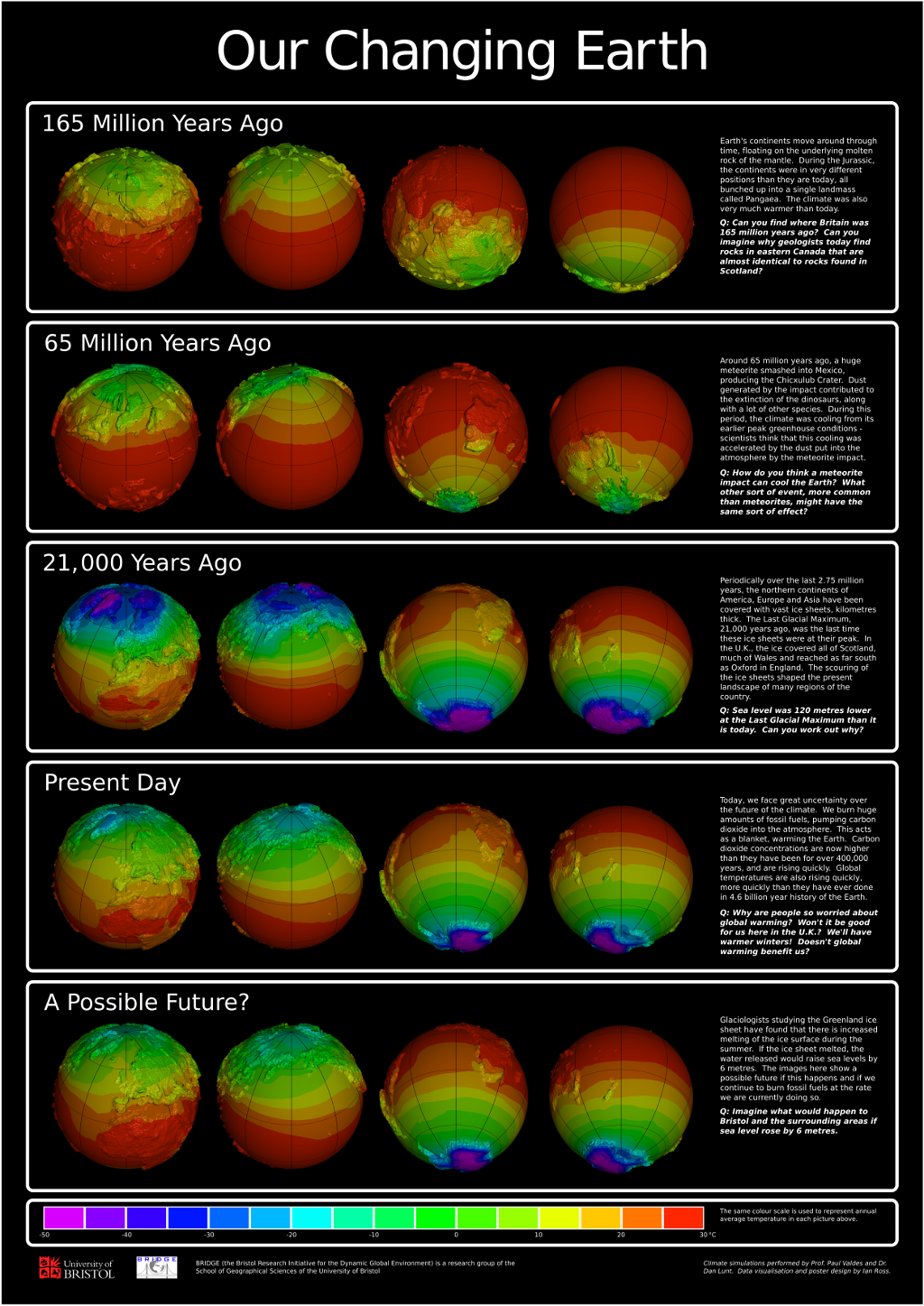
I also discovered that POV-Ray is great for making simple visuals– the geometric language used by POV-Ray is really easy to use for building small models, and using a ray tracer means that support for transparency is built-in. A simple schematic picture of the El Niño cycle demonstrates this. More complex things I’ve done like this include representations of interesting bathymetric features in the Mediterranean that we used for a proposal about the application of a new type of ocean model to flows in complex bathymetry. I used the same triangulation methods for the earth views on the paleogeography poster at the bottom of the page.
Posters
And sometimes, you need to put a whole bunch of images together into a poster. Here are a couple of examples, one about paleogeography and paleoclimate for a public outreach event, and the other about El Niño behaviour in the PMIP2 models for a scientific meeting.

 Simple regression plots
Simple regression plots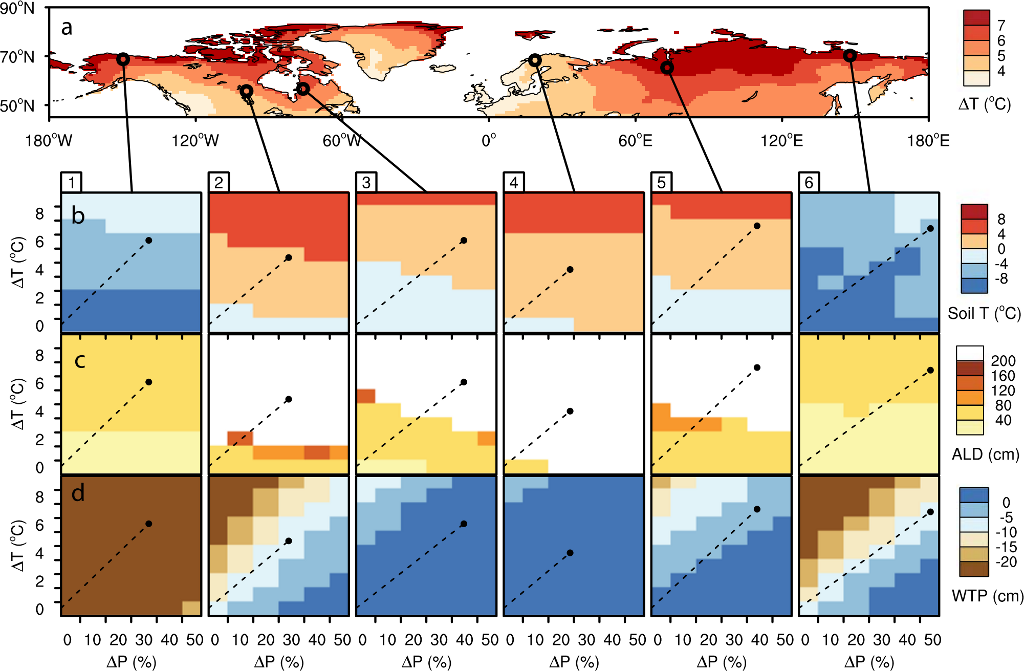 LPJ-WHyMe climate sensitivity
LPJ-WHyMe climate sensitivity LPJ-WHyMe regression results
LPJ-WHyMe regression results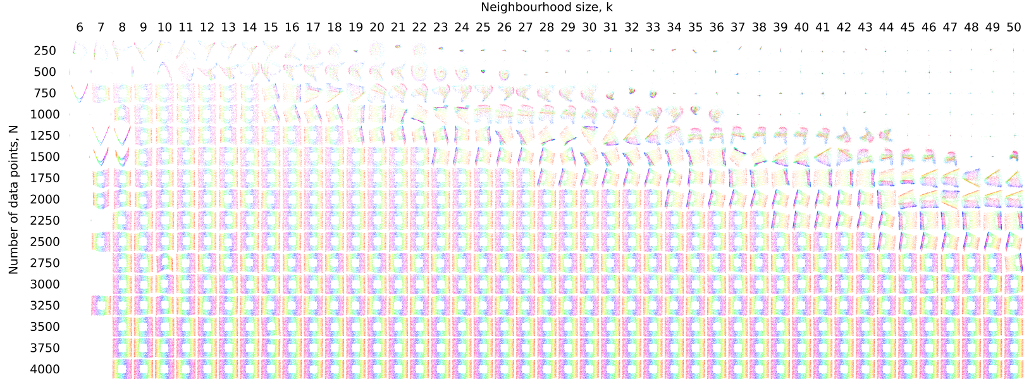
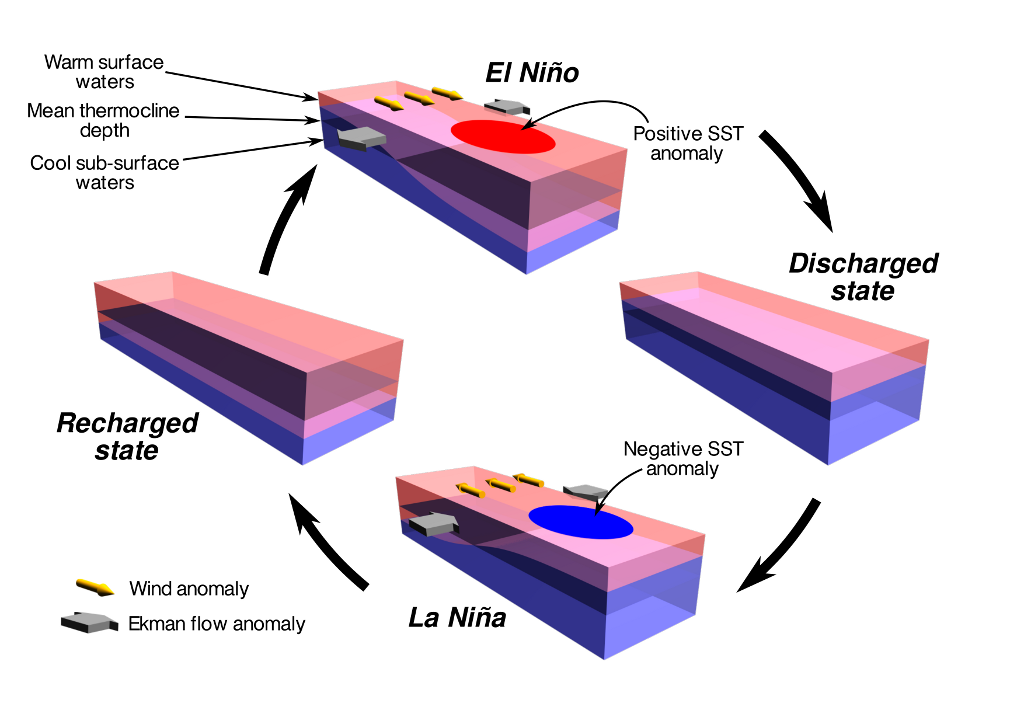 ENSO cartoons
ENSO cartoons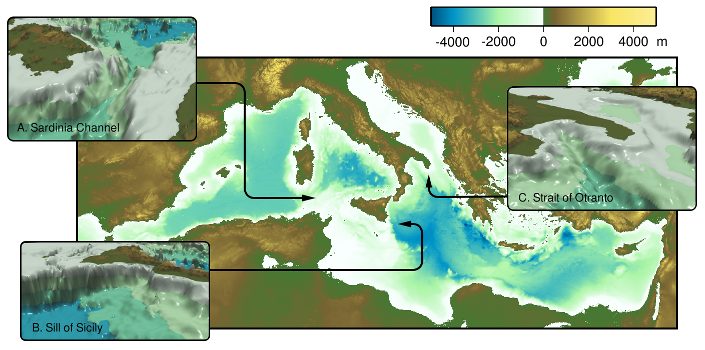 Mediterranean bathymetry
Mediterranean bathymetry