Non-diffusive atmospheric flow #5: pre-processing
Note: there are a couple of earlier articles that I didn’t tag as “haskell” so they didn’t appear in Planet Haskell. They don’t contain any Haskell code, but they cover some background material that’s useful to know (#3 talks about reanalysis data and what $Z_{500}$ is, and #4 displays some of the characteristics of the data we’re going to be using). If you find terms here that are unfamiliar, they might be explained in one of these earlier articles.
The code for this post is available in a Gist.
Update: I missed a bit out of the pre-processing calculation here first time round. I’ve updated this post to reflect this now. Specifically, I forgot to do the running mean smoothing of the mean annual cycle in the anomaly calculation–doesn’t make much difference to the final results, but it’s worth doing just for the data manipulation practice...
Before we can get into the “main analysis”, we need to do some pre-processing of the $Z_{500}$ data. In particular, we are interested in large-scale spatial structures, so we want to subsample the data spatially. We are also going to look only at the Northern Hemisphere winter, so we need to extract temporal subsets for each winter season. (The reason for this is that winter is the season where we see the most interesting changes between persistent flow regimes. And we look at the Northern Hemisphere because it’s where more people live, so it’s more familiar to more people.) Finally, we want to look at variability about the seasonal cycle, so we are going to calculate “anomalies” around the seasonal cycle.
We’ll do the spatial and temporal subsetting as one pre-processing step and then do the anomaly calculation seperately, just for simplicity.
Spatial and temporal subsetting
The title of the paper we’re trying to follow is “Observed Nondiffusive Dynamics in Large-Scale Atmospheric Flow”, so we need to decide what we mean by “large-scale” and to subset our data accordingly. The $Z_{500}$ data from the NCEP reanalysis dataset is at 2.5° × 2.5° resolution, which turns out to be a little finer than we need, so we’re going to extract data on a 5° × 5° grid instead. We’ll also extract only the Northern Hemisphere data, since that’s what we’re going to work with.
For the temporal subsetting, we need to take 181 days of data for each year starting on 1 November each year. Since the data starts at the beginning of 1948 and goes on to August 2014 (which is when I’m writing this), we’ll have 66 years of data, from November 1948 until April 2014. As usual when handling dates, there’s some messing around because of leap years, but here it basically just comes down to which day of the year 1 November is in a given year, so it’s not complicated.
The daily NCEP reanalysis geopotential height data comes in one file per year, with all the pressure levels used in the dataset bundled up in each file. That means that the geopotential height variable in each file has coordinates: time, level, latitude, longitude, so we need to slice out the 500 mb level as we do the other subsetting.
All this is starting to sound kind of complicated, and this brings us to a regrettable point about dealing with this kind of data–it’s messy and there’s a lot of boilerplate code to read and manipulate coordinate metadata. This is true pretty much whatever language you use for processing these multi-dimensional datasets and it’s kind of unavoidable. The trick is to try to restrict this inconvenient stuff to the pre-processing phase by using a consistent organisation of your data for the later analyses. We’re going to do that here by storing all of our $Z_{500}$ anomaly data in a single NetCDF file, with 151-day long winter seasons back-to-back for each year (151 days rather than 181 because we’re going to lose 15 days at either end of each year of data due to some smoothing that we’re going to do in the seasonal cycle removal). This will make time and date processing trivial.
The code for the data subsetting is in the subset.hs program in the Gist. We’ll deal with it in a few bites.
Skipping the imports that we need, as well as a few “helper” type synonym definitions, the first thing that we need to do it open one of the input NCEP NetCDF files to extract the coordinate metadata information. This listing shows how we do this:
Right refnc <- openFile $ indir </> "hgt.1948.nc" let Just nlat = ncDimLength <$> ncDim refnc "lat" Just nlon = ncDimLength <$> ncDim refnc "lon" Just nlev = ncDimLength <$> ncDim refnc "level" let (Just lonvar) = ncVar refnc "lon" (Just latvar) = ncVar refnc "lat" (Just levvar) = ncVar refnc "level" (Just timevar) = ncVar refnc "time" (Just zvar) = ncVar refnc "hgt" Right lon <- get refnc lonvar :: SVRet CFloat Right lat <- get refnc latvar :: SVRet CFloat Right lev <- get refnc levvar :: SVRet CFloat
We open the first of the NetCDF files (I’ve called the directory where I’ve stored these things indir) and use the hnetcdf ncDim and ncVar functions to get the dimension and variable metadata for the latitude, longitude, level and time dimensions; we then read the complete contents of the “coordinate variables” (for level, latitude and longitude) as Haskell values (here, SVRet is a type synonym for a storable vector wrapped up in the way that’s returned from the hnetcdf get functions).
Once we have the coordinate variable values, we need to find the index ranges to use for subsetting. For the spatial subsetting, we find the start and end ranges for the latitudes that we want (17.5°N-87.5°N) and for the level, we find the index of the 500 mb level:
let late = vectorIndex LT FromEnd lat 17.5 lats = vectorIndex GT FromStart lat 87.5 levi = vectorIndex GT FromStart lev 500.0
using a helper function to find the correspondence between coordinate values and indexes:
data IndexStart = FromStart | FromEnd vectorIndex :: (SV.Storable a, Ord a) => Ordering -> IndexStart -> SV.Vector a -> a -> Int vectorIndex o s v val = case (go o, s) of (Nothing, _) -> (-1) (Just i, FromStart) -> i (Just i, FromEnd) -> SV.length v - 1 - i where go LT = SV.findIndex (>= val) vord go GT = SV.findIndex (<= val) vord vord = case s of FromStart -> v FromEnd -> SV.reverse v
For the temporal subsetting, we just work out what day of the year 1 November is for leap and non-leap years–since November and December together are 61 days, for each winter season we need those months plus the first 120 days of the following year:
let inov1non = 305 - 1 -- ^ Index of 1 November in non-leap years. wintertsnon = [0..119] ++ [inov1non..365-1] -- ^ Indexes of all winter days for non-leap years. inov1leap = 305 + 1 - 1 -- ^ Index of 1 November in leap years. wintertsleap = [0..119] ++ [inov1leap..366-1] -- ^ Indexes of all winter days for leap years. winterts1948 = [inov1leap..366-1] winterts2014 = [0..119] -- ^ Indexes for winters in start and end years.
This is kind of hokey, and in some cases you do need to do more sophisticated date processing, but this does the job here.
Once we have all this stuff set up, the critical part of the subsetting is easy–for each input data file, we figure out what range of days we need to read, then use a single call the getS from hnetcdf (“get slice”):
forM_ winterts $ \it -> do -- Read a slice of a single time-step of data: Northern -- Hemisphere (17.5-87.5 degrees), 5 degree resolution, 500 -- mb level only. let start = [it, levi, lats, 0] count = [1, 1, (late - lats) `div` 2 + 1, nlon `div` 2] stride = [1, 1, 2, 2] Right slice <- getS nc zvar start count stride :: RepaRet2 CShort
Here, we have a set of start indexes, a set of counts and a set of strides, one for each dimension in our input variable. Since the input geopotential height files have dimensions of time, level, latitude and longitude, we have four entries in each of our start, count and stride lists. The start values are the current day from the list of days we need (called it in the code), the level we’re interested in (levi), the start latitude index (lats) and zero, since we’re going to get the whole range of longitude. The count list gets a single time step, a single level, and a number of latitude and longitude values based on taking every other entry in each direction (since we’re subsetting from a spatial resolution of 2.5° × 2.5° to a resolution of 5° × 5°). Finally, for the stride list, we use a stride of one for the time and level directions (which doesn’t really matter anyway, since we’re only reading a single entry in each of those directions) and a stride of two in the latitude and longitude directions (which gives us the “every other one” subsetting in those directions).
All of the other code in the subsetting program is involved in setting up the output file and writing the $Z_{500}$ slices out. Setting up the output file is slightly tedious (this is very common when dealing with NetCDF files–there’s always lots of metadata to be managed), but it’s made a little simpler by copying attributes from one of the input files, something that doing this in Haskell makes quite a bit easier than in Fortran or C. The next listing shows how the NcInfo for the output file is created, which can then be passed to the hnetcdf withCreateFile function to actually create the output file:
let outlat = SV.fromList $ map (lat SV.!) [lats,lats+2..late] outlon = SV.fromList $ map (lon SV.!) [0,2..nlon-1] noutlat = SV.length outlat noutlon = SV.length outlon outlatdim = NcDim "lat" noutlat False outlatvar = NcVar "lat" NcFloat [outlatdim] (ncVarAttrs latvar) outlondim = NcDim "lon" noutlon False outlonvar = NcVar "lon" NcFloat [outlondim] (ncVarAttrs lonvar) outtimedim = NcDim "time" 0 True outtimeattrs = foldl' (flip M.delete) (ncVarAttrs timevar) ["actual_range"] outtimevar = NcVar "time" NcDouble [outtimedim] outtimeattrs outz500attrs = foldl' (flip M.delete) (ncVarAttrs zvar) ["actual_range", "level_desc", "valid_range"] outz500var = NcVar "z500" NcShort [outtimedim, outlatdim, outlondim] outz500attrs outncinfo = emptyNcInfo (outdir </> "z500-subset.nc") # addNcDim outlatdim # addNcDim outlondim # addNcDim outtimedim # addNcVar outlatvar # addNcVar outlonvar # addNcVar outtimevar # addNcVar outz500var
Although we can mostly just copy the coordinate variable attributes from one of the input files, we do need to do a little bit of editing of the attributes to remove some things that aren’t appropriate for the output file. Some of these things are just conventions, but there are some tools that may look at these attributes (actual_range, for example) and may complain if the data doesn’t match the attribute. It’s easier just to remove the suspect ones here.
This isn’t pretty Haskell by any means, and the hnetcdf library could definitely do with having some higher-level capabilities to help with this kind of file processing. I may add some based on the experimentation I’m doing here–I’m developing hnetcdf in parallel with writing this!
Anyway, the result of running the subsetting program is a single NetCDF file containing 11946 days (66 × 181) of $Z_{500}$ data at a spatial resolution of 5° × 5°. We can then pass this on to the next step of our processing.
Seasonal cycle removal
In almost all investigations in climate science, the annual seasonal cycle stands out as the largest form of variability (not always true in the tropics, but in the mid-latitudes and polar regions that we’re looking at here, it’s more or less always true). The problem, of course, is that the seasonal cycle just isn’t all that interesting. We learn about the difference between summer and winter when we’re children, and although there is much more to say about seasonal variations and how they interact with other phenomena in the climate system, much of the time they just get in the way of seeing what’s going on with those other phenomena.
So what do we do? We “get rid” of the seasonal cycle by looking at what climate scientists call “anomalies”, which are basically just differences between the values of whatever variable we’re looking at and values from a “typical” year. For example, if we’re interested in daily temperatures in Innsbruck over the course of the twentieth century, we construct a “typical” year of daily temperatures, then for each day of our 20th century time series, we subtract the “typical” temperature value for that day of the year from the measured temperature value to give a daily anomaly. Then we do whatever analysis we want based on those anomalies, perhaps looking for inter-annual variability on longer time scales, or whatever.
This approach is very common, and it’s what we’re going to do for our Northern Hemisphere winter-time $Z_{500}$ data here. To do this, we need to do two things: we need to calculate a “typical” annual cycle, and we need to subtract that typical annual cycle from each year of our data.
OK, so what’s a “typical” annual cycle? First, let’s say a word about what we mean by “annual cycle” in this case. We’re going to treat each spatial point in our data independently, trusting to the natural spatial correlation in the geopotential height to smooth out any shorter-term spatial inhomogeneities in the typical patterns. We then do some sort of averaging in time to generate a “typical” annual cycle at each spatial point. It’s quite common to use the mean annual cycle over a fixed period for this purpose (a period of 30 years is common: 1960-1990, say). In our case, we’re going to use the mean annual cycle across all 66 years of data that we have. Here’s how we calculate this mean annual cycle (this is from the seasonal-cycle.hs program in the Gist):
-- Each year has 181 days, so 72 x 15 x 181 = 195480 data values. let ndays = 181 nyears = ntime `div` ndays -- Use an Int array to accumulate values for calculating mean annual -- cycle. Since the data is stored as short integer values, this is -- enough to prevent overflow as we accumulate the 2014 - 1948 = 66 -- years of data. let sh = Repa.Z Repa.:. ndays Repa.:. nlat Repa.:. nlon slicecount = [ndays, nlat, nlon] zs = take (product slicecount) (repeat 0) init = Repa.fromList sh zs :: FArray3 Int -- Computation to accumulate a single year's data. let doone current y = do -- Read one year's data. let start = [(y - 1948) * ndays, 0, 0] Right slice <- getA innc z500var start slicecount :: RepaRet3 CShort return $! Repa.computeS $ current Repa.+^ (Repa.map fromIntegral slice) -- Accumulate all data. total <- foldM doone init [1948..2013] -- Calculate the final mean annual cycle. let mean = Repa.computeS $ Repa.map (fromIntegral . (`div` nyears)) total :: FArray3 CShort
Since each year of data has 181 days, a full year’s data has 72 × 15 × 181 data values (72 longitude points, 15 latitude points, 181 days), i.e. 195,480 values. In the case here, since we have 66 years of data, there are 12,901,680 data values altogether. That’s a small enough number that we could probably slurp the whole data set into memory in one go for processing. However, we’re not going to do that, because there are plenty of cases in climate data analysis where the data sets are significantly larger than this, and you need to do “off-line” processing, i.e. to read data from disk piecemeal for processing.
We do a monadic fold (using the standard foldM function) over the list of years of data, and for each year we read a single three-dimensional slice of data representing the whole year and add it to the current accumulated sum of all the data. (This is what the doone function does: the only slight wrinkle here is that we need to deal with conversion from the short integer values stored in the data file to the Haskell Int values that we use in the accumulator. Otherwise, it’s just a question of applying Repa’s element-wise addition operator to the accumulator array and the year’s data.) Once we’ve accumulated the total values across all years, we divide by the number of years and convert back to short integer values, giving a short integer valued array containing the mean annual cycle–a three-dimensional array with one entry for each day in our 181-day winter season and for each latitude and longitude in the grid we’re using.
We’re also going to use a 31-day running mean to smooth the annual cycle at each spatial point. This only makes a little difference to the results, but we do it to follow the analysis in the paper. The runmean function we use to do this is shown here:
runmean :: FArray3 CShort -> Int -> FArray3 CShort runmean x d = computeS $ traverse x (const smshape) doone where (Z :. nz :. ny :. nx) = extent x -- ^ Extent of input array. smshape = Z :. nz - 2 * d :. ny :. nx -- ^ Extent of smoothed output array: spatial dimensions are -- the same as the input, and just the time dimension is -- reduced by the averaging. sz = Z :. (2 * d + 1) :. 1 :. 1 -- ^ Slice extent for averaging. len = fromIntegral (2 * d + 1) :: Double -- ^ Averaging length. dem x = fromIntegral (truncate x :: Int) -- ^ Type demotion from Double to CShort for output. pro :: Array U DIM3 Double pro = computeS $ map (\x -> fromIntegral (fromIntegral x :: Int)) x -- ^ Type promotion of input from CShort to Double. doone _ i = dem $ (sumAllS (extract i sz pro)) / len -- ^ Calculate a single averaged value.
It uses the Repa traverse function to calculate a 31-day box-car average at each relevant space and time point. There’s a little bit of tricky type conversion going on to make sure that we can do the averaging and to make sure that we get back a CShort array as output, but other than that it’s not too complicated. (We do the promotion from CShort to Double once, into the value I’ve called pro to avoid repeated conversion from short integer values to floating point values.) The running mean calculation means that we lose 15 days at either end of each year of data, so that each year of anomalies is 151 days.
Once we have the mean annual cycle with which we want to calculate anomalies, determining the anomalies is simply a matter of subtracting the mean annual cycle from each year’s data, matching up longitude, latitude and day of year for each data point. The next listing shows the main loop that does this, reading a single day of data at a time, then subtracting the appropriate slice of the mean annual cycle to produce anomaly values (Repa’s slice function is handy here) and writing these to an output NetCDF file:
-- Process one input year at a time, accumulating all relevant -- time-steps into a single output file. itoutref <- newIORef 0 :: IO (IORef Int) let count = [1, nlat, nlon] forM_ [0..ntime-1] $ \it -> do -- If "it" is within the 151 day winter block... when (it `mod` 181 >= 15 && it `mod` 181 <= 165) $ do -- Read time slice. Right sli <- getA innc z500var [it, 0, 0] count :: RepaRet2 CShort -- Calculate anomalies and write out. let isl = it `mod` 181 - 15 sl = Z :. isl :. All :. All anom = computeS $ sli -^ (slice smoothmean sl) :: FArray2 CShort itout <- readIORef itoutref putStrLn $ show it ++ " -> " ++ show itout modifyIORef itoutref (+1) putA outnc outtimevar [itout] [1] (SV.slice it 1 time) putA outnc outz500var [itout, 0, 0] count anom return ()
There are only two things we have to be a little bit careful about here. First, when we create the final anomaly output file is that we need to remove some of the attributes from the $Z_{500}$ variable: because we’re now working with differences between actual values and our “typical” annual cycle, we no longer need the add_offset and scale_factor attributes that are used to convert from the stored short integer values to floating point geopotential height values. Instead, the values that we store in the anomaly file are the actual geopotential height anomaly values in metres. Second, we’re going from seasons of 181 days of data to seasons of 151 days (because we only calculate anomalies for days for which we have a smoothed seasonal cycle), so we need to do a little work to keep track of the different indexes we’re using.
After doing all this pre-processing, what we end up with is a single NetCDF file containing 66 winter seasons of daily $Z_{500}$ anomalies for the region we’re interested in. The kind of rather boring data processing we’ve had to do to get to this point is pretty typical for climate data processing–you almost always need to do some sort of subsetting of your data, you often want to remove signals that aren’t interesting (like the annual cycle here, although things can get much more complicated than that). This kind of thing is unavoidable, and the best that you can really do is to try to organise things so that you do the pre-processing once and end up with data in a format that’s then easy to deal with for further processing. That’s definitely the case here, where we have fixed-length time series (151 days per winter) for each year, so we don’t need to do any messing around with dates.
In other applications, pre-processing can be a much bigger job. For functional brain imaging applications, for example, as well as extracting a three-dimensional image from the output of whatever (MRI or CT) scanner you’re using, you often need to do something about the low signal-to-noise ratios that you get, you need to compensate for subject motion in the scanner during the measurements, you need to compensate for time-varying physiological nuisance signals (breathing and heart beat), you need to spatially warp images to match an atlas image to enable inter-subject comparison, and so on. And all that is before you get to doing whatever statistical analysis you’re really interested in.
We will look at some of these “warts and all” pre-processing cases for other projects later on, but for now the small amount of pre-processing we’ve had to do here is enough. Now we can start with the “main analysis”.
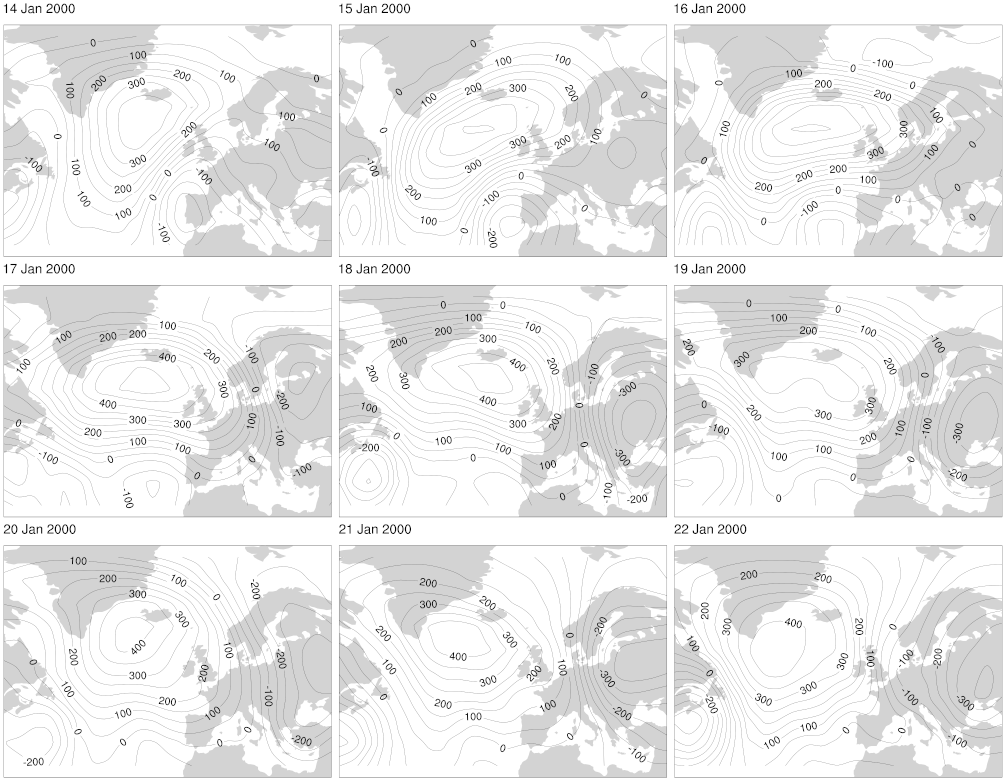
Before we do that though, let’s take a quick look at what these anomaly values look like. The two figures below show anomaly plots for the same time periods for which the original $Z_{500}$ data is shown in the plots in this earlier article. The “normal” anomaly plots are a bit more variable than the original $Z_{500}$ plots, but the persistent pattern over the North Atlantic during the blocking episode in the second set of plots is quite clear. This gives us some hope that we’ll be able to pick out these persistent patterns in the data relatively easily.
First, the “normal” anomalies:
then the “blocking” anomalies: