Non-diffusive atmospheric flow #12: dynamics warm-up
The analysis of preferred flow regimes in the previous article is all very well, and in its way quite illuminating, but it was an entirely static analysis–we didn’t make any use of the fact that the original $Z_{500}$ data we used was a time series, so we couldn’t gain any information about transitions between different states of atmospheric flow. We’ll attempt to remedy that situation now.
What sort of approach can we use to look at the dynamics of changes in patterns of $Z_{500}$? Our $(\theta, \phi)$ parameterisation of flow patterns seems like a good start, but we need some way to model transitions between different flow states, i.e. between different points on the $(\theta, \phi)$ sphere. Each of our original $Z_{500}$ maps corresponds to a point on this sphere, so we might hope that we can some up with a way of looking at trajectories of points in $(\theta, \phi)$ space that will give us some insight into the dynamics of atmospheric flow.
Since atmospheric flow clearly has some stochastic element to it, a natural approach to take is to try to use some sort of Markov process to model transitions between flow states. Let me give a very quick overview of how we’re going to do this before getting into the details. In brief, we partition our $(\theta, \phi)$ phase space into $P$ components, assign each $Z_{500}$ pattern in our time series to a component of the partition, then count transitions between partition components. In this way, we can construct a matrix $M$ with
$$ M_{ij} = \frac{N_{i \to j}}{N_{\mathrm{tot}}} $$ where $N_{i \to j}$ is the number of transitions from partition $i$ to partition $j$ and $N_{\mathrm{tot}}$ is the total number of transitions. We can then use this Markov matrix to answer some questions about the type of dynamics that we have in our data– splitting the Markov matrix into its symmetric and antisymmetric components allows us to respectively look at diffusive (or irreversible) and non-diffusive (or conservative) dynamics.
Before trying to apply these ideas to our $Z_{500}$ data, we’ll look (in the next article) at a very simple Markov matrix calculation by hand to get some understanding of what these concepts really mean. Before that though, we need to take a look at the temporal structure of the $Z_{500}$ data–in particular, if we’re going to model transitions between flow states by a Markov process, we really want uncorrelated samples from the flow, and our daily $Z_{500}$ data is clearly correlated, so we need to do something about that.
Autocorrelation properties
Let’s look at the autocorrelation properties of the PCA projected component time series from our original $Z_{500}$ data. We use the autocorrelation function in the statistics package to calculate and save the autocorrelation for these PCA projected time series. There is one slight wrinkle–because we have multiple winters of data, we want to calculate autocorrelation functions for each winter and average them. We do not want to treat all the data as a single continuous time series, because if we do we’ll be treating the jump from the end of one winter to the beginning of the next as “just another day”, which would be quite wrong. We’ll need to pay attention to this point when we calculate Markov transition matrices too. Here’s the code to calculate the autocorrelation:
npcs, nday, nyear :: Int npcs = 10 nday = 151 nyear = 66 main :: IO () main = do -- Open projected points data file for input. Right innc <- openFile $ workdir </> "z500-pca.nc" let Just ntime = ncDimLength <$> ncDim innc "time" let (Just projvar) = ncVar innc "proj" Right (HMatrix projsin) <- getA innc projvar [0, 0] [ntime, npcs] :: HMatrixRet CDouble -- Split projections into one-year segments. let projsconv = cmap realToFrac projsin :: Matrix Double lens = replicate nyear nday projs = map (takesV lens) $ toColumns projsconv -- Calculate autocorrelation for one-year segment and average. let vsums :: [Vector Double] -> Vector Double vsums = foldl1 (SV.zipWith (+)) fst3 (x, _, _) = x doone :: [Vector Double] -> Vector Double doone ps = SV.map (/ (fromIntegral nyear)) $ vsums $ map (fst3 . autocorrelation) ps autocorrs = fromColumns $ map doone projs -- Generate output file. let outpcdim = NcDim "pc" npcs False outpcvar = NcVar "pc" NcInt [outpcdim] M.empty outlagdim = NcDim "lag" (nday - 1) False outlagvar = NcVar "lag" NcInt [outlagdim] M.empty outautovar = NcVar "autocorr" NcDouble [outpcdim, outlagdim] M.empty outncinfo = emptyNcInfo (workdir </> "autocorrelation.nc") # addNcDim outpcdim # addNcDim outlagdim # addNcVar outpcvar # addNcVar outlagvar # addNcVar outautovar flip (withCreateFile outncinfo) (putStrLn . ("ERROR: " ++) . show) $ \outnc -> do -- Write coordinate variable values. put outnc outpcvar $ (SV.fromList [0..fromIntegral npcs-1] :: SV.Vector CInt) put outnc outlagvar $ (SV.fromList [0..fromIntegral nday-2] :: SV.Vector CInt) put outnc outautovar $ HMatrix $ (cmap realToFrac autocorrs :: Matrix CDouble) return ()
We read in the component time series as a hmatrix matrix, split the matrix into columns (the individual component time series) then split each time series into year-long segments. The we use the autocorrelation function on each segment of each time series (dropping the confidence limit values that the autocorrelation function returns since we’re not so interested in those here) and average across segments of each time series. The result is an autocorrelation function (for lags from zero to $\mathtt{nday}-2$) for each PCA component. We write those to a NetCDF file for further processing.
The plot below shows the autocorrelation functions for the first three PCA projected component time series. The important thing to notice here is that there is significant autocorrelation in each of the PCA projected component time series out to lags of 5–10 days (the horizontal line on the plot is at a correlation of $e^{-1}$). This makes sense–even at the bottom of the atmosphere, where temporal variability tends to be less structured than at 500\,mb, we expect the weather tomorrow to be reasonably similar to the weather today.
It appears that there is pretty strong correlation in the $Z_{500}$ data at short timescales, which would be an obstacle to performing the kind of Markov matrix analysis we’re going to do next. To get around this, we’re going to average our data over non-overlapping 7-day windows (seven days seems like a good compromise between throwing lots of data away and reducing the autocorrelation to a low enough level) and work with those 7-day means instead of the unprocessed PCA projected component time series. This does mean that we now need to rerun all of our spherical PDF analysis for the 7-day mean data, but that’s not much of a problem because everything is nicely scripted and it’s easy to rerun it all.
Spherical PDF for 7-day means
The figures below show the same plots as we earlier had for all the PCA projected component time series, except this time we’re looking at the 7-day means of the projected component time series, to ensure that we have data without significant temporal autocorrelation.
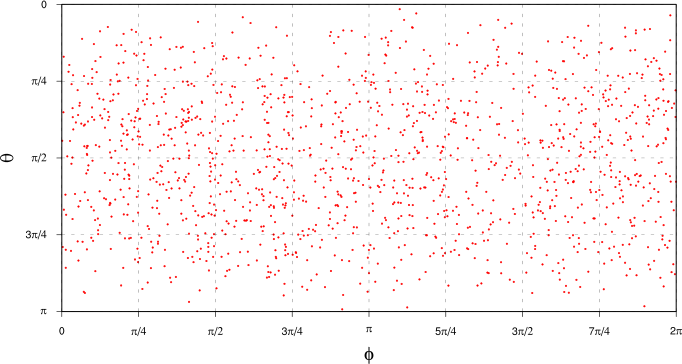
The first figure tab (“Projected points”) shows the individual 7-day mean data points, plotted using $(\theta, \phi)$ polar coordinates. Comparing with the corresponding plot for all the data in the earlier article, we can see (obviously!) that there’s less data here, but also that it’s not really any easier to spot clumping in the data points than it was when we used all the data. It again makes sense to do KDE to find a smooth approximation to the probability density of our atmospheric flow patterns.
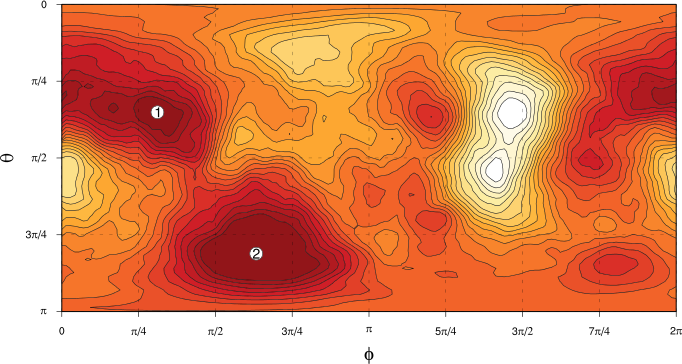
The “Spherical PDF” tab shows the spherical PDF of 7-day mean PCA components (parametrised by spherical polar coordinates $\theta$ and $\phi$) calculated by kernel density estimation: darker colours show regions of greater probability density. Two “bumps” are labelled for further consideration. Compared to the “all data” PDF, the kernel density estimate of the probability density for the 7-day mean data is more concentrated, with more of the probability mass appearing in the two labelled bumps on the plot. (Recall that the “all data” PDF had four “bumps” that we picked out to look at–here we only really have two clear bumps.)
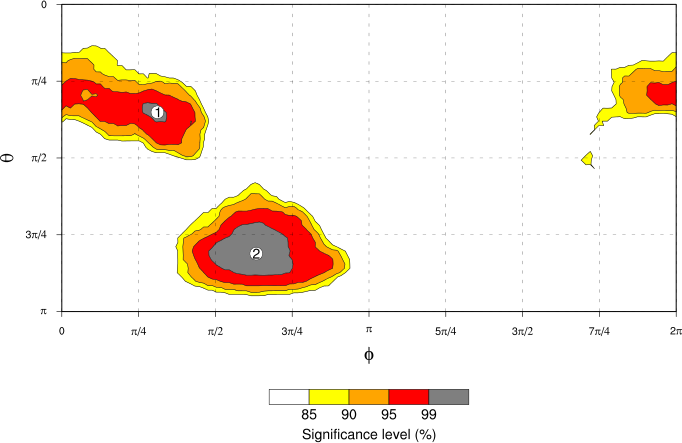
We can determine the statistical significance of those bumps in exactly the same way as we did before. The “Significance” tab above shows the results. As you’d expect, both of the labelled bumps are highly significant. However, notice that the significance scale here extends only to 99\% significance, while that for that “all data” case extends to 99.9%. The reduced significance levels are simply a result of having less data points–we have 1386 7-day mean points as compared to 9966 “all data” points, which means that we have more sampling variability in the null hypothesis PDFs that we use to generate the histograms used for the significance calculation. That increased sampling variability translates into less certainty that our “real data” couldn’t have occurred by chance, given the assumptions of the null hypothesis. Still, 99% confidence isn’t too bad!
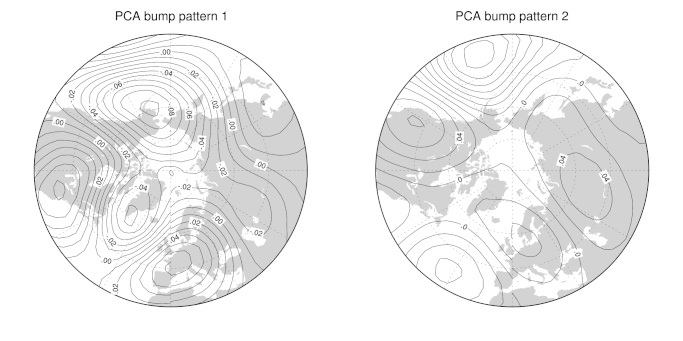
Finally, we can plot the spatial patterns of atmospheric flow corresponding to the labelled bumps in the PDF, just as we did for the “all data” case. The “Bump patterns” tab shows the patterns for the two most prominent bumps in the 7-day means PDF. As before, the two flow patterns seem to distinguish quite clearly between “normal” zonal flow (in this case, pattern #2) and blocking flow (pattern #1).
Now that we’ve dealt with this autocorrelation problem, we’re ready to start thinking about how we model transitions between different flow states. In the next article, we’ll use a simple low-dimensional example to explain what we’re going to do.